O comprimento original da barra é 300 quando está reta. Se ela for submetida a uma deformação por cisalhamento definida por onde é dado em milímetros, determine o deslocamento na extremidade de sua borda inferior. A barra foi distorcida até a forma mostrada, na qual não ocorre alongamento na direção

Passo 1
Primeiro, temos que perceber que a deformação é dada por uma função. Por isso, devemos trabalhar com a variação desta função. Ou seja, uma derivada para encontrarmos o . Fica assim:
Passo 2
Para a gente se livrar dessa derivação vamos aplicar a integração dos dois lados. E substituindo a função dada.
Passo 3
Para encontrarmos os limites de integração, vamos dar uma olhada na figura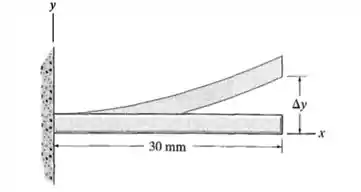
Da pra ver que o o varia entre e o varia entre
Passo 4
Resolvendo essa integral, encontramos