Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 63
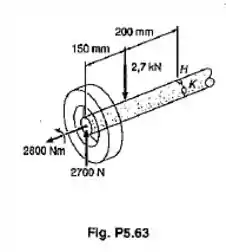
O eixo mecânico de um automóvel é feito para suportar as forças e o torque mostrado. Sabendo-se que o diâmetro do eixo é de 30 mm, determinar as tensões, normal e de cisalhamento, no: (a) ponto H; (b) ponto K.
Passo 1
Do enunciado temos que o eixo tem 30 mm de diâmetro, então
Temos que calcular
Calculando J então
Com isso podemos calcular
Passo 2
Até agora foi tranquilo, agora vamos analizar os momentos. Observa que temos 2. Vamos ter
Então para o total
Podemos então calcular o
Precisaremos então do momento de inércia
Então calculando agra
Passo 3
Podemos agora fazer uma análise dos sinais pra os pontos H e K
a) Ponto H
b) Ponto K
Resposta
Exercícios de Livros Relacionados
Selecione no Apêndice B a viga estrutural de abas largas de menor peso e menor altura que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é σ a d m = 168M P a e a
Selecione no Apêndice B a viga de aço de abas largas de menor peso que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é σ a d m = 168M P a e a tensão de cisalhame
Determine, com aproximação de múltiplos de 5 mm, a largura mínima da viga que suportará com segurança a carga P = 40 k N . A tensão de flexão admissível é σ a d m = 168M P a e a tensão de cisalhamento
Selecione no Apêndice B a viga de aço de abas largas de menor peso e altura que suportará com segurança as cargas mostradas na figura, na qual w = 0 e P = 50k N . A tensão de flexão admissível é σ a d
Trace os diagramas de força cortante e momento fletor para a viga W310x21 e verifique se ela suportará com segurança a carga mostrada na figura. A tensão de flexão admissível é σ a d m = 160M P a e a