Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 62
O frustum do cone está em balanço a partir do ponto . Se o cone é feito de um material tendo peso específico de , determine a força cortante e o momento fletor interno no cone como uma função de .
Passo 1
O problema quer que a gente encontre o esforço cortante e o momento fletor no cone usando uma função.
Vamos começar usando a semelhança de triangulo para pegarmos algumas informações:
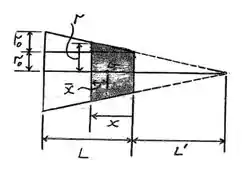
E:
Ou seja:
Passo 2
Agora, vamos logo calcular o volume do frustum, que nada mais é do que um tronco de cone:
Passo 3
O peso do frustrum é:
E também precisamos encontrar o centro de massa no eixo :
Usando um diagrama de corpo livre, vamos calcular a força e o momento:
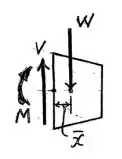
Então, vamos para o momento:
Resposta
Exercícios de Livros Relacionados
Calcule a força em cada membro da treliça carregada.
Determine as forças nos membros A B , B C e B D da treliça carregada.
Calcule a força em cada membro da treliça carregada.
Determine a força em cada membro da treliça carregada.
Determine a força em cada membro da treliça carregada. Todos os triângulos são isósceles.