Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 90

9.09 Determine a área da superfície e o volume do sólido formado girando-se a área sombreada 360 ° em torno do eixo z .

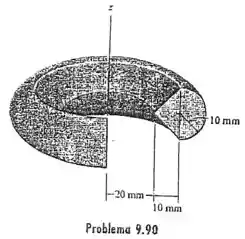
Passo 1

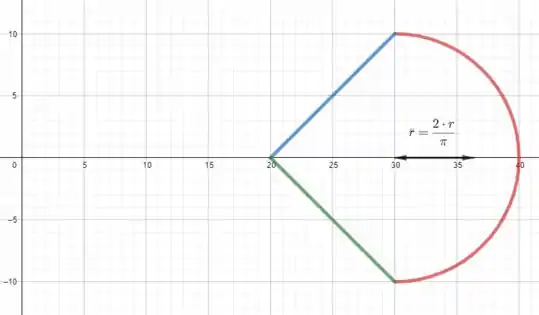
Para gerarmos essa superfície devemos fazer a revolução de 2 segmentos de reta e um arco de circunferência:

A fórmula para determinar a área superficial é:

A = θ ∑ r - L

Onde θ é o ângulo de revolução em radianos, nesse caso 2 π

r - é a distância perpendicular do eixo de revolução, nesse caso o eixo z , ao centroide da curva de geração.

O centroide de uma segmento de reta fica sempre no seu centro, então é fica fácil de calcularmos:

r - a z u l = 20 + 1 0 2 = 25   m m

r - v e r d e = 20 + 10 2 = 25   m m

E o controide do arco de circunferência é tabelado, então o r - vai ficar

r - v e r m e l h o = 30 + 2 R π

r - v e r m e l h o = 30 + 2 10 π

r - v e r m e l h o = 36,37   m m

E L é o comprimento da curva de geração. Para as retas podemos usar pitagoras:

L a z u l 2 = 1 0 2 + 1 0 2

L a z u l = 2 00 = 10 2   m

L v e r d e 2 = 1 2 + 1 2

L v e r d e = 2 00 = 10 2   m

E a parte vermelha é metade de uma circunferência de raio 10:

L v e r m e l h o = 1 2 ⋅ 2 π R

L v e r m e l h o = π 10

L v e r m e l h o = 3 1 , 42   m m

Passo 2

Agora só multiplicar aplicar na fórmula:

A = 2 π 25 ⋅ 10 2 + 25 ⋅ 10 2 + 36,67 ⋅ 31 , 42

A = 11 , 7 ⋅ 10 3   m m 2

Passo 3

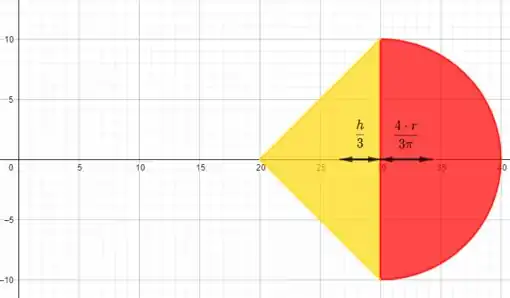
E para calcular o volume, vamos separar o sólido em um triângulo e um semi circulo, para fazer a revolução deles:

A fórmula para determinar o volume é:

V = θ ∑ r - A

Onde θ é o ângulo de revolução em radianos, nesse caso 2 π

r - é a distância perpendicular do eixo de revolução ao centroide da área de geração. O centroide de um retângulo fica bem no meio dele, então

r - a m a r e l o = 30 - h 3

r - a m a r e l o = 30 - 10 3

r - a m a r e l o = 26,67   m m

e

r - v e r m e l h o = 30 + 4 ⋅ r 3 π

r - v e r m e l h o = 30 + 4 ⋅ 10 3 π

r - v e r m e l h o = 34,24   m m

E A é a área de geração, ou seja a área de cada formato:

A a m a r e l o = b h 2

A a m a r e l o = 20 10 2

A a m a r e l o = 100   m m 2

e

A v e r m e l h o = 1 2 ⋅ π r 2

A v e r m e l h o = 1 2 ⋅ π 10 2

A v e r m e l h o = 157,1   m m 2

Passo 4

Então é só aplicar na formula e obteremos o volume:

V = θ ∑ r - A

V = 2 π 26,67 100 + 34,24 157,1

V = 50 , 6 ⋅ 10 3   m m 3

Resposta

A = 11,7 ⋅ 10 3   m m 2

V = 50,6 ⋅ 10 3   m m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo horizontal de aço com dois diâmetros é soldado ao bloco fixo em A . Construa os diagramas de cisalhamento e momento no eixo devido ao seu peso. Determine os valores da força cortante e do momen
Determine a massa e a localização do centroide do corpo de alumínio fundido.
As seções triangulares e retangulares estão sendo consideradas para o projeto de uma pequena barragem de concreto de água doce. Do ponto de vista da resistência ao capotamento em torno de C, qual seçã
O casco de aço semicilíndrico com extremidades fechadas tem uma massa de 26,6 kg. Determine a massa m do lastro de chumbo que deve ser colocado na concha de modo que ele flutue em água doce em sua pro
Uma estrutura projetada para observação da vida marinha sob o gelo em águas polares consiste em uma câmara de visualização cilíndrica conectada à superfície por um eixo cilíndrico aberto na parte supe