Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas de Revisão - Ex. 157

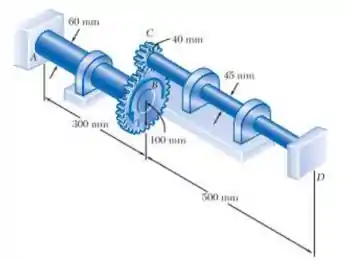
As extremidades A e D dois eixos sólidos AB e CD são fixas, enquanto as extremidade B e C são conectadas por engrenagens conforme mostrado. Sabendo que a tensão de cisalhamento admissível é de 50 MPa em cada eixo, determine o maior torque T que pode ser aplicado à engrenagem B.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine o maior torque T que pode ser aplicado à engrenagem B. Para isso vamos esboçar essas engrenagens ;)

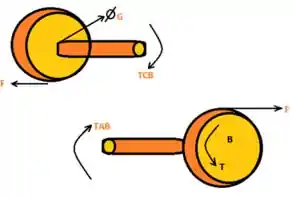
Considerando as engrenagens B e C:

∅ B = r C r B = 40 100 ∅ C                 ∅ B = 0,4 ∅ C

Vamos fazer o somatório do momento em c e em B ;)

M C = 0 :       T C D = r C F ∑ M B = 0 :       T -   T A B = r B F

Consideramos que:

T -   T A B = r B r C T C D               T = T A B + 100 40 T C D T = T A B + 2,5 T C D  

Eixo AB: L = 0,3   m ,           c = 0,030   m ∅ B = ∅ B / A = T A B L J G = T A B   x   ( 0,3 ) π 2   x   ( 0,030 ) 4 G = 235,77   x   10 3 T A B G

Eixo CD: L = 0,5   m ,           c = 0,0225   m ∅ C = ∅ C / D = T C D L J G = T C D   x   ( 0,5 ) π 2   x   ( 0,0225 ) 4 G = 1242   x   10 3 T C D G

Passo 2

Entao gurizada, falta pouquinho, vem comigo ;)

∅ B = 0,4 ∅ C :         235,79   x   10 3 T A B G = 0,4   x   1242   x     10 3 T C D G T C D = 0,47462   T A B

Substituindo T C D temos:

T = T A B + 2,5   x   ( 0,47462   T A B )

Resolvendo para T A B temos:

T = 2,1865   x   T C D 0,47462

Tensão para o eixo AB:

τ A B = τ a l l = 50 M P a τ A B = T A B C J         T A B = J C τ A B = π 2 c 3 τ A B = π 2   x   0,030 m 3   x   50   x   10 6 P a = 2120,6   N * m E a torção é:

T = 2,1865   x   2120,6   N * m = 4,64   k N * m

Passo 3

Para a tensão para eixo CD:

τ C D = τ a l l = 50 M P a τ C D = T C D C J         T C D = π 2 c 3 τ C D = π 2   x   0,0225 m 3 x   50   x   10 6 P a = 894,62   N * m

E o torque temos:

T = 4,6068   x   894,62   N * m = 4,12   k N * m

O menor valor para T governa.

Resposta

T = 2,1865   T A B T = 4,6068   T C D T = 4,12   k N * m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo composto tem uma seção média que indica o eixo maciço de 20m m de diâmetro e um tubo soldado a flanges rígidas em A e B . Despreze a espessura das flanges e determine o ângulo de torção da extr
Resolva o Problema 5.68 se o torque distribuído for t = ( k x 2 // 3 ) N . m // m .
O parafuso de aço A-36 é apertado dentro de um furo de modo que o torque de reação na haste A B pode ser expresso pela equaçãot=( k x ² )N . m / m ² , onde x é dado em metros. Se um torque T=50N . m f
O tubo de bronze C 86100 tem diâmetro externo de 37,5m m e espessura de 3m m . A conexão em C está sendo apertada com uma chave de torque. Se for aplicada uma força F=100N , determine a tensão de cisa
O eixo é feito de aço-ferramenta L2, tem diâmetro de 40m m e está preso em suas extremidades A e B . Se for submetido ao conjugado, determine a tensão de cisalhamento máxima nas regiões A C e C B .