Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 104
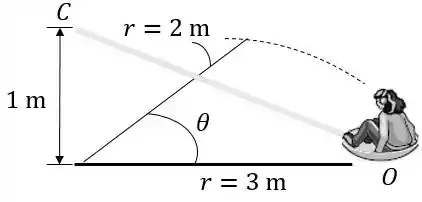
Um garoto parado firmemente em pé gira a garota sentada em um ‘prato’ circular ou trenó em uma trajetória circular de raio m de tal maneira que sua velocidade angular é rad/s. Se o cabo de conexão é puxado para dentro de tal maneira que a coordenada radial varia com uma velocidade constante de m/s, determine a tração que ele exerce sobre o trenó no instante que m. O trenó e a garota têm massa total de 50 kg. Despreze a dimensão da garota e do trenó e os efeitos do atrito entre o trenó e o gelo. Dica: primeiro, demonstre que a equação do movimento na direção resulta em
Quando integrado, , onde a constante é determinada a partir dos dados do problema.
Passo 1
O Problema nos deu as seguintes informações:
Massa total:
Trajetória circular de raio inicial: m
Velocidade angular: rad/s
Velocidade constante em : m/s
A questão pede para determinarmos a tração que o cabo exerce sobre o trenó no instante que m.
Desenhamos o seguinte diagrama de corpo livre:
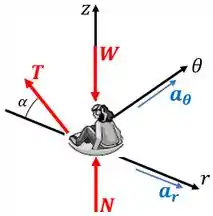
Onde é a força peso e , é a força normal e é a força exercida pelo cabo .
Passo 2
O enunciado nos dá a dica de iniciar pela demonstração de
Sabemos que
Podemos dizer que é igual a seguinte derivada:
Aplicando a Equação do Movimento em , temos que
Logo,
Integrando está equação, obtemos
Onde é uma constante qualquer.
O enunciado nos informa que, quando integrado, .
Passo 3
Agora iremos substituir valores das condições iniciais na relação .
Temos que, para , . Logo,
A questão pede para resolvermos o problema para m. Logo, temos que
Para , também sabemos que m/s e é constante. Portanto, .
Passo 4
Agora temos dados suficientes para encontrar .
Passo 5
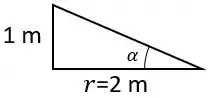
Em seguida, devemos encontrar o valor do âgulo que faz com o eixo quando m.
Analisando a geometria da figura fornecida, temos que
Passo 6
Aplicaremos as Equações do Movimento no eixo .