Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 20

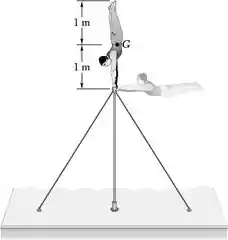
Um ginasta de 80 kg está executando uma série de giros completos em uma barra horizontal. Na posição mostrada na figura, ele tem velocidade angular pequena e desprezível e manterá seu corpo ereto e rígido à medida que girar para baixo. Admitindo que, durante o giro, o raio de giração centroidal de seu corpo seja de 0,4 m, determine a velocidade angular e a força exercida sobre suas mãos após ele ter girado (a) 90°, (b) 180°.

Passo 1

O enunciado pede que a gente determine a velocidade angular e a força exercida sobre suas mãos após ele ter girado (a) 90°, (b) 180°.

Posição 1. (Diretamente acima da barra).

Elevação:

h = 3.5   ft

Energia potencial:

V 1 = W h 1 = 160   lb 3.5   ft = 560   ft ∙ lb

Velocidades:

ω 1 = 0 ,               v - 1 = 0

Energia cinética:

T 1 = 0

Passo 2

  1. Posição 2. (Corpo no nível da barra após girar 90 ° )

    2. Elevação:

    h 2 = 0

    Energia potencial:

    V 2 = 0

    Velocidades:

    v - 2 = 1.1 ω 2

    Energia cinética:

    T 2 = 1 2 m v - 2 2 + 1 2 m k 2 ω 2 2

    T 2 = 1 2 16 32.2 3.5 ω 2 2 + 1 2 160 32.2 1.5 2 ω 2 2 = 36.025 ω 2 2

    Passo 3

    Princípio da conservação de energia.

    T 1 + V 1 = T 2 + V 2 :               0 + 560 = 36.025 ω 2 2

    ω 2 2 = 15.545

    Cinemática:

    a - t = 3.5 α

    a - n = 3.5 ω 2 2 = 3.5 15.545 = 54.407   ft/ s 2   ←

    + Σ M 0 = Σ M 0 eff :                 3.5 160 = 160 32.2 3.5 3.5 α + 160 32.2 1.5 2 α

    α = 7.7724   rad/ s 2                 a - t = 27.203   ft/ s 2 ↓

    ← + Σ F x = m a n :               R x = 160 32.2 54.407 = 270.35   lb ←

    ← + Σ F y = - m a t :               R y - 160 = - 160 32.2 27.203 ↑

    R y = 24.83   lb ↑

    Passo 4

  2. Posição 3. (Diretamente abaixo da barra após girar 180 ° )

Elevação:

h 3 = - 1.1   m

Energia potencial:

V 3 = W h 3 = 160   lb - 3.5 = - 560   ft ∙ lb

Velocidades:

v - 3 = 3.5 ω 3

Energia cinética:

T 3 = 36.025 ω 3 2

Princípio da conservação da energia.

T 1 + V 1 = T 3 + V 3 :               0 + 560 = 36.025 ω 2 2 - 560

ω 3 2 = 31.09

Cinemática:

a n = 3.5 31.09 = 108.81   ft/ s 2 ↑

A partir de

Σ M 0 = Σ M 0 eff                 e                 Σ F x = 0 ,

α = 0 ,               a t = 0               R x = 0

+ ↑ Σ F y = m a n :               R y - 160 = 160 32.2 108.81 ↑

R y = 700.62   lb

Resposta

a )   ω 2 = 3.94   rad/s  

R = 271   lb     5.25 °

b )   ω 3 = 5.58   rad/s  

R = 701   lb↑

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um concentrador experimental de energia solar por lentes Fresnelpode girar em torno do eixo horizontal AB que passa por meio deseu centro de massa G. Ele é suportado em A e B por uma estruturaque pode
Uma hélice de quatro lâminas de um avião tem massa de 160 kg e raio de giração de 800 mm. Sabendo que a hélice gira a 1.600 rpm quando o avião voa em uma trajetória circular vertical de 600 m de raio
A engrenagem A de 950 -g é restrita a rolar na engrenagem fixa B, mas é livre para girar em torno do eixo AD. O eixo AD, de comprimento 400 mm e massa desprezível, é conectado por uma manilha ao eixo
O eixo do Problema 18.67 está inicialmente em repouso ( ω = 0), quando um binário de momento M0 é aplicado a ele. Sabendo que a resultante da aceleração angular é α = (20 rad/s2)i, determine (a) o bin
O conjunto do Problema 18.68 está inicialmente em repouso ( ω = 0), quando um binário de momento M0 é aplicado ao eixo AB. Sabendo que a aceleração angular resultante do conjunto é α = (150 rad/s2)i,