Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 76

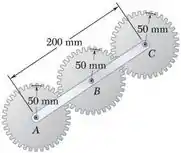
No arranjo das engrenagens mostrado na figura, as engrenagens A e C estão presas à barra ABC, que é livre para girar em torno de B, enquanto a engrenagem interna B é fixa. Sabendo que o sistema está em repouso, determine a intensidade do binário M que deve ser aplicado na barra ABC se 2,5 s depois a velocidade angular da barra for de 240 rpm no sentido horário. As engrenagens A e C têm massa de 1,25 kg cada uma e podem ser consideradas como discos de raio de 50 mm; a barra ABC tem massa de 2 kg.

Passo 1

O enunciado pede que a gente determine a intensidade do binário M que deve ser aplicado na barra ABC se 2,5 s depois a velocidade angular da barra for de 240 rpm no sentido horário. As engrenagens A e C têm massa de 1,25 kg cada uma e podem ser consideradas como discos de raio de 50 mm; a barra ABC tem massa de 2 kg.

Seja ω A B C = ω

v _ A = v _ C = B C ω = 2 r ω

Uma vez que as engrenagens A e C rolam na engrenagem fixa B,

ω A = ω C = v C r = 2 r ω r = 2 ω

Passo 2

Princípio de impulso e momentum.

+ Momentos sobre D:

0 + Q t r = m C v _ C r + I _ C w C

Q t r = m C 2 r ω r + 1 2 m C r 2 2 ω

Q t = 3 m C r w

Passo 3

+ Momentos sobre B:

M t - Q t 4 r = I _ A B C ω

M t - 4 Q t r = 1 12 m A B C 4 r 2 ω

M t - 4 Q t r = 4 3 m A B C r 2 ω

Passo 4

Substitua por (Qt) de (1) em (2):

M t - 4 3 m C r ω r = 4 3 m A B C r 2 ω

M t = 4 3 r 2 ω m A B C + 9 m C

Casal M.

Dados:

t = 2.5   s

r = 2 12   f t

m A B C = 4   l b 32.2   f t / s

m C = 2.5   l b 32.2   f t / s 2

ω = 240   r p m

= 8 π   r a d / s

Eq. (3):

M = 2.5   s = 4 3 2 12 f t 2 8 π   r a d / s 4 32.2 + 9 2.5 33.2

2.5   M = 0.76607

M = 0.3064   l b ∙ f t

Resposta

M = 0.306   l b ∙ f t  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esferaAde 700 g, movendo-se com velocidadev0paralela ao chão, atinge a face inclinada de uma cunhaBde 2,1 kg, inicialmente em repouso, que pode rolar livremente sobre o chão. Após o impacto, é obs
Os três blocos mostrados na figura são idênticos. Os blocosBeCestão em repouso quando o blocoBé atingido pelo blocoA, que se move com uma velocidadevAde 3 m/s. Após o impacto, considerado perfeitament
Quando a corda está a um ângulo de α=30 ° a esferaAde 1 kg tem uma velocidadev0= 0,6 m/s. O coeficiente de restituição entreAe cunhaBde 2 kg é 0,8 e o comprimento da cordal= 1 m. A constante da mola t
Os blocos A e B têm massa de 0,5 kg cada, e o bloco C de 1,5 kg. O coeficiente de atrito entre os blocos e o plano é k =0,30. Inicialmente, o bloco A move-se a uma velocidade vo= 4 m/s e os blocos B e
Uma bolaBde 70 g é largada de uma alturah0= 1,5 m e alcança uma alturah2= 0,25 m após dois quiques em placas idênticas de 210 g.AplacaArepousa diretamente no chão duro, ao passo que a placaCrepousa so