Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 110
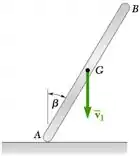
Resolva o Problema 17.109, considerando que o impacto entre a barra AB e a superfície sem atrito é perfeitamente elástico.
Passo 1
O enunciado pede que a gente Resolva o Problema 17.109, considerando que o impacto entre a barra AB e a superfície sem atrito é perfeitamente elástico.
Momento de inércia.
Impacto perfeitamente elástico.
Passo 2
Componentes horizontais:
Componentes de velocidade :
Momentos sobre A:
Resposta
Exercícios de Livros Relacionados
As pequenas esferas, que possuem as massas e velocidades iniciais indicadas na figura, atingem e tornam-se presas às extremidades pontudas da haste, que é livremente articulada em O e está inicialment
Em um dado instante, a partícula de massa m tem a posição e a velocidade mostradas na figura, e sofre a ação da força F . Determine sua quantidade de movimento angular em torno do ponto O e a taxa de
O conjunto parte do repouso e atinge uma velocidade angular de 150r p m sob a ação de uma força T de 20N aplicada à corda por t segundos. Determine t . Despreze o atrito e todas as massas exceto a das
A esfera de 3k g se desloca no plano x - y e tem a velocidade indicada em um determinado instante. Determine sua ( a ) quantidade de movimento linear, ( b ) quantidade de movimento angular em torno do
A única força atuando sobre um satélite da Terra que se desloca fora da atmosfera terrestre é a atração gravitacional radial. O momento desta força é nulo em torno do centro da Terra tomado como um po