Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 11
Uma partícula move-se ao longo de uma linha reta com uma velocidade onde é dado em segundos. Quando , a partícula está localizada à esquerda da origem. Determine a aceleração quando , o deslocamento de para e a distância que a partícula percorre durante este período.
Passo 1
Para uma dada velocidade, nada mais fácil do que calcular a aceleração! Basta derivar:
Logo, em , a aceleração fica
Passo 2
Agora, para determinar a posição para uma velocidade dada, tampouco tem mistério: basta usar a relação e em seguida obter o . Olha só:
Integrando entre e , obtemos
Resolvendo, ficamos com
Assim o deslocamento entre e vale
Passo 3
Agora tem pegadinha! CUIDADO! A distância total percorrida em 10 segundos é simplesmente o valor de em ? NÃOOOO!
Não te esquece de que representa apenas a POSIÇÃO a partir da origem! A distância sempre será dada como uma variação de .
É neste ponto que devemos usar a condição de que, quando , a partícula está localizada à esquerda da origem (). De fato, pela equação que deduzimos, isto significa que
Dai, , logo, a nossa equação pra fica
De fato, esboçando um gráfico de em função de , temos algo assim:
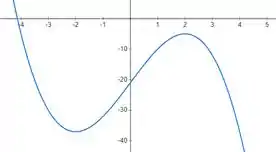
Agora fica mais clara a pergunta: Quantos metros de fato caminhamos entre e ?
Bem, pelo gráfico, dá pra ver que a distância total percorrida entre e é
Por outra parte, a distância entre e deve ser de
Daí, a distância requerida é
Dai,