Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas fundamentais - Ex. 5
Determine a força máxima que pode ser aplicada sem causar o movimento da caixa de 100 kg com centro de gravidade em . O coeficiente de atrito estático no piso é .
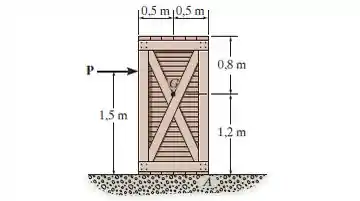
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão bem tranquila. Precisamos determinar a força máxima para que a caixa não se movimente.
Para isto, temos que garantir que ela não tombe e ela não deslize!
E para que a gente analise os dois casos, basta utilizarmos as equações de equilíbrio (e trabalhar um pouco com as hipóteses para cada caso).
Então, vamos as contas!
Passo 2
Vamos começar determinando a força máxima para que não haja deslizamento. Aqui, a força de atrito máxima será igual a força .
Portanto, aplicando as equações de equilíbrio, temos:
E assim obtemos a força máxima para que a caixa não deslize!
Passo 3
Já para garantir que não há tombamento, é necessário que o somatório dos momentos em torno do ponto (quina da caixa no piso) seja nulo! Portanto,
Como o menor valor obtido para foi 327 N, então essa é a nossa força máxima!
E assim finalizamos a questão!