Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas fundamentais - Ex. 3
Determine a força máxima que pode ser aplicada sem causar o movimento das duas caixas de 50 kg. O coeficiente de atrito estático entre cada caixa e o piso é .
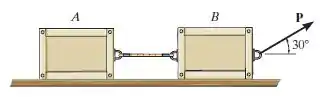
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão bem tranquila. Queremos determinar qual a força máxima que não cause o movimento das duas caixas.
Para isto, basta analisarmos as forças nas duas caixas separadamente, garantindo que a força de atrito é máxima.
Então, vamos as contas!
Passo 2
Vamos começar pela caixa . Esboçando o seu diagrama de corpo livre, temos:
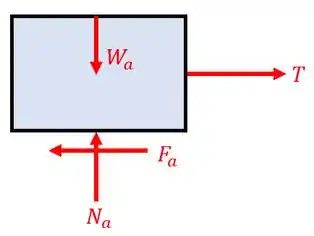
Sendo a força peso, a força normal, a força de atrito e a tração no cabo.
Como a caixa está em equilíbrio, ao aplicarmos as equações de equilíbrio nós obtemos:
E assim paramos de trabalhar com o bloco .
Passo 3
Agora temos que repetir o mesmo procedimento para o bloco . Portanto,
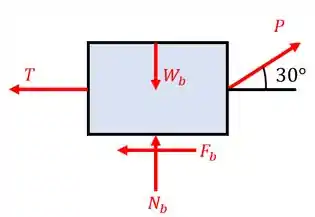
Novamente, aplicando as equações de equilíbrio, temos:
Substituindo a segunda equação na primeira, nós obtemos:
E assim finalizamos a questão!