Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 80
Determine a intensidade de de modo que o momento de binário resultante seja , em sentido anti-horário. Em que ponto sobre a viga o momento de binário resultante atua?
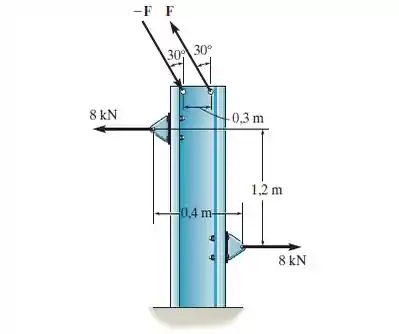
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta questão possui duas perguntas: determinar a intensidade da força e em que ponto o momento de binário é aplicado. Então, temos uma pergunta de cálculo e uma teórica!
Não vamos nos assustar aqui. Vamos começar devagar pela parte do cálculo que vai dar tudo certo!
Sabemos que o momento de binário resultante, devido os 2 binários, é igual a . A chave para trabalharmos com binários é identificarmos a distância perpendicular as forças.
Para isto, as vezes é necessário decompormos as forças, o que é o caso desta questão. Decompondo as forças , temos o seguinte diagrama:
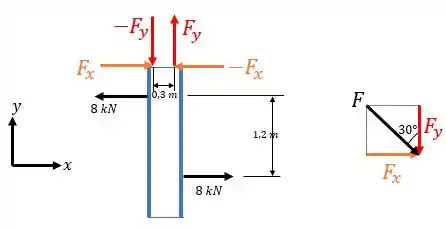
Percebam a relação da decomposição da força ao lado para deixar mais claro ainda!
Passo 2
Agora que já interpretamos toda a geometria, já podemos partir para as contas. Vamos começar calculando as forças e . Elas são:
Como as duas forças e são colineares, elas não produzem um momento para o nosso problema. Aqui, apenas as forças com uma distância de .
Percebam que aqui nós não determinarmos o comprimento perpendicular as forças opostas . Se a gente tivesse feito assim, o trabalho seria muito maior! Aqui a gente está se livrando de um problemão!
Portanto, o binário desta força é:
Passo 3
Para descobrirmos a intensidade da força , vamos ter que utilizar a relação da intensidade do momento de binário resultante. Sabemos que:
Sendo o momento resultante pela força de .
Está aqui é moleza. Pela própria geometria já sabemos que a distância perpendicular é . Portanto,
Então, a força que buscamos é:
E assim finalizamos a primeira parte da questão!
Passo 4
Por fim, basta respondermos a parte teórica da questão: sobre qual ponto o momento de binário resultante atua. Aqui é a parte mais fácil de toda questão: qualquer ponto!!!
O momento de binário é um vetor livre. Ele causa o mesmo efeito rotacional em um corpo, independentemente do ponto de aplicação!
Resposta
O momento de binário resultante pode ser aplicado sobre qualquer ponto.