Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 45
O homem usa o carrinho de mão para subir o material pelo degrau. Se o carrinho e seu conteúdo possuem massa de 50 kg com centro de gravidade em , determine a reação normal nas duas rodas e a intensidade e direção da força mínima exigida no punho necessárias para levantar a carga.
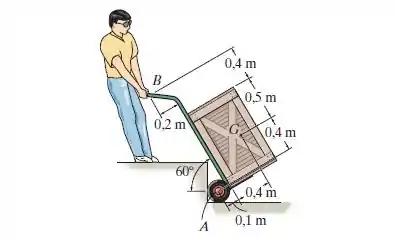
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a reação normal nas duas rodas e a intensidade e direção da força mínima exigida em para levantar a carga.
Para isto, é fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!! Então, o nosso diagrama de equilíbrio será:
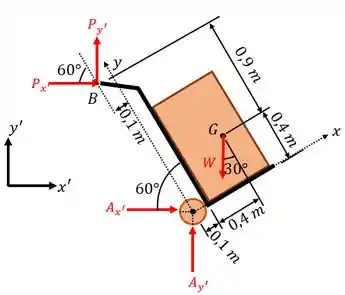
A chave para resolvermos esta questão está em dois pontos: O sistema de coordenadas e e a força normal .
Vamos começar pela parte mais fácil. Para que o carrinho descole do chão, a força deve ser igual a zero. Portanto, para qualquer cálculo nosso, devemos desconsiderá-la.
Já em relação a escolha do sistema de coordenadas, ele pode facilitar e muito as nossas contas. As vezes o sistema e tradicional facilita as contas. Em outros momentos, é o sistema e inclinado que facilita.
Para esta questão, vamos trabalhar com ambos os sistemas, sendo cada um deles no seu momento ideal.
Bom, agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Vamos começar determinando a força necessária para que o carrinho seja levantado. Vamos começar calculando . Para isto, basta fazermos o somatório de forças na direção . Portanto,
Já para calcularmos , temos que fazer o somatório dos momentos em torno do ponto . Neste caso já facilita trabalharmos com o sistema inclinado. Portanto,
Portanto, a força necessária é:
E ela forma um ângulo com a direção positiva do eixo .
Passo 3
Para finalizarmos a questão, basta fazermos o somatório de forças na direção . Portanto,
E assim finalizamos a questão!
Resposta
A força necessária para levantar o carrinho é e ela forma um ângulo com a direção positiva do eixo . A força normal nas rodas é .