Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 81

A haste central C D do conjunto é aquecida de T 1 = 30   ° C até T 2 = 180   ° C por resistência elétrica. As duas hastes A B e E F situadas nas extremidades também são aquecidas de T 1 = 30   ° C   até T 2 = 5 0   ° C . Na temperatura mais baixa, T 1 , a folga entre C e a barra rígida é 0 , 7   mm . Determine a força nas hastes A B e E F provocada pelo aumento na temperatura. As hastes A B e E F são feitas de aço e cada uma tem área de seção transversal de 125   mm 2 . C D é feita de alumínio e tem área de seção transversal de 375   mm 2 . E a ç o = 200   GPa , E a l = 70   GPa , α a ç o = 12 10 - 6 / ° C , α a l = 23 10 - 6 / ° C .

Passo 1

Uma barra rígida está apoiada em duas hastes de aço, A B e E F . Uma haste central C D está posicionada abaixo da barra rígida com uma folga de δ = 0,7   mm . A haste C D sofre uma mudança de temperatura Δ T a l . As hastes A B e E F sofrem uma mudança de temperatura Δ T a l .

Características das hastes A B e E F :

  • Aço: E a ç o = 200   GPa , α a ç o = 12 10 - 6   ° C - 1 .
    • Área transversal: A a ç o = 125   mm 2 .
    • Comprimento inicial: L a ç o = 300   mm .
    • Temperatura inicial: T a ç o , 1 = 30   ° C . Temperatura final T a ç o , 2 = 5 0   ° C .

      • Características da haste C D :

    • Alumínio: E a l = 70   GPa , α a l = 23 10 - 6   ° C - 1 .
  • Área transversal: A a l = 375   mm 2 .
  • Comprimento inicial: L a l = 240   mm .
  • Temperatura inicial: T a l , 1 = 30   ° C . Temperatura final T a l , 2 = 180   ° C .

Muita informação! Vamos com calma!

A variação de temperatura Δ T a l = 180 - 30 = 150   ° C irá causar expansão térmica na haste C D , aumentando um comprimento δ T C D . Quando esse avanço superar a folga δ , a haste C D estará pressionando sobre a barra rígida com uma força F C .

Além disso, a variação de temperatura Δ T a ç o = 5 0 - 30 = 2 0   ° C irá causar expansão térmica nas hastes A B e E F , aumentando cada uma delas um comprimento δ T a ç o .

A barra se moverá para cima, esticando as hastes A B e E F . Essas hastes de aço resistem à tração com forças F B e F F .

Queremos descobrir essas forças!

Passo 2

Vamos ver como fica o diagrama de corpo livre.

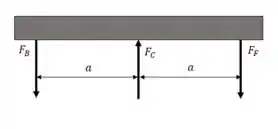
Não sabemos aquele comprimento a na figura, mas não importa! O que interessa é a simetria, veja: fazendo o equilíbrio de momentos ao redor do centro C , temos

∑ M C = 0     →     a ⋅ F B = a ⋅ F F     →     F B = F F

Show, pra facilitar vamos chamar de F a ç o = F B = F F .

Agora vejamos o equilíbrio de forças:

∑ F = 0     →     F C = 2 ⋅ F a ç o

Temos duas incógnitas e uma equação. Vamos buscar outra equação pela compatibilidade de deslocamentos.

Passo 3

Vejamos o que acontece com a haste C D :

  • O aumento de temperatura Δ T a l vai causar uma expansão: δ T C D
  • A haste C D vai primeiro cobrir a folga δ = 0,7   mm . Depois disso, ela pressiona a barra.
  • A haste C D vai empurrar a barra. A barra vai resistir com uma força F C , reduzindo: δ F C D .

    • Agora, vejamos os efeitos nas hastes A B e E F :

  • O aumento de temperatura Δ T a ç o vai causar uma expansão: δ T a ç o
  • A barra está subindo, tracionando com uma força F a ç o as hastes A B e E F . Isso as estica: δ F a ç o .

Vamos dizer que o total que a haste de alumínio C D aumenta é δ C D = δ T C D - δ F C D .

E o total que as hastes de aço aumentam é δ a ç o = δ T a ç o + δ F a ç o .

Juntando isso tudo:

δ a ç o = δ C D - δ

δ T a ç o + δ F a ç o = δ T C D - δ F C D - δ

Beleza, a parte difícil já foi. Agora é só fórmula!

Passo 4

Temos fórmulas pra todos esses termos na compatibilidade! Expansão térmica:

δ T = α   Δ T   L

Relação carga-deslocamento:

δ F = F   L A   E

α a ç o   Δ T a ç o   L a ç o + F a ç o   L a ç o A a ç o   E a ç o = α a l   Δ T a l   L a l - F C   L a l A a l   E a l - δ

Aplicando os valores, temos:

0,072   mm + 12 ⋅ 10 - 6  mm/N ⋅ F a ç o = 0,828   mm - 9,143 ⋅ 10 - 6   mm/N ⋅ F C -   0,7   mm

Queremos a força F a ç o , então vamos isolar ela:

F a ç o = 4 , 667   kN - 0,762 F C

Passo 5

Quase lá! Substitua a relação encontrada no equilíbrio de forças:

F C = 2 ⋅ F a ç o     →     F a ç o = 4 , 667 2,524   kN

F a ç o = 1 , 849   kN

Resposta

Força nas hastes A B e E F : F B = F F = 1,849   kN .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa de concreto de alta resistência utilizada em uma pista de rolamento tem 6m de comprimento quando sua temperatura é 10° C . Se houver uma folga de 3mm em um de seus lados antes de tocar seu a
Os dois segmentos de haste circular, um de alumínio e outro de cobre, estão presos às paredes rígidas de tal modo que há uma folga de 0,2mm entre eles quando T 1 = 15° C . Cada haste tem diâmetro de 3
O tubo de bronze 86100 tem raio interno de 12,5mm e espessura de parede de 5mm . Se o gás que passa por ele mudar a temperatura do tubo uniformemente de T A = 60° C em A para T B = 15° C em B , determ
O tubo de aço A- 36 está acoplado aos colares em A e B . Quando a temperatura é 15° C , não há nenhuma carga axial no tubo. Se o gás quente que passa pelo tubo provocar uma elevação de Δ T = 20 + 30 x
Uma trena de aço é usada por um supervisor para medir o comprimento de uma reta. A seção transversal da trena é retangular, com 1,25mm de espessura por 5mm de largura, e o comprimento é 30m quando T 1