Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 9
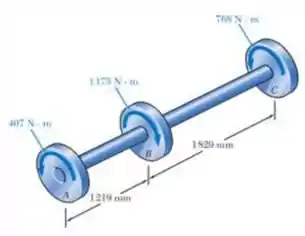
Os torques mostrados são aplicados às polias A, B e C. Sabendo que os eixos têm seção cheia, determine a máxima tensão de cisalhamento (a) no eixo AB e (b) no eixo BC.
Passo 1
E ai gurizada tudo belezinha?? O exercício pede para que a gente determine a máxima tensão de cisalhamento nos eixos AB e BC, então partiu!!!
Vamos começar pelo eixo AB
Onde J é dada por:
Sendo o torque calculado como:
Substituindo os valores temos:
Passo 2
Então agora seguimos para o eixo BC!
Onde J é dada por:
Substituindo os valores temos:
Resposta
Exercícios de Livros Relacionados
O tubo é submetido a um torque de 750 N · m. Determine a parcela desse torque à qual a seção sombreada cinza resiste. Resolva o problema de duas maneiras: (a) usando a fórmula da torção e (b) determin
Um eixo maciço de raio r está sujeito a um torque T . Determine o raio r ' do núcleo interno do eixo que resista a 1 / 4 do torque aplicado ( T / 4 ). Resolva o problema de duas maneiras: a usando a f
Um eixo maciço de 30mm de diâmetro é usado para transmitir os torques aplicados às engrenagens. Determine a tensão de cisalhamento máxima absoluta no eixo.
O eixo tem diâmetro de 80mm e, devido ao atrito na superfície no interior do furo, está sujeito a um torque variável descrito pela função t = 25 x ⋅ e x 2Nm/m , onde x é dado em metros. Determine o to
O elo funciona como parte do controle do elevador de um pequeno avião. Se o tubo de alumínio conectado tiver 25mm de diâmetro interno e parede de 5mm de espessura, determine a tensão de cisalhamento m