Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 27
O eixo está apoiado em suas extremidades por dois mancais, e , e está sujeito às forças aplicadas às polias nele fixadas. Determine as cargas internas resultantes que agem na seção transversal que passa pelo ponto . As forças de agem na direção e as forças de e agem na direção . Os apoios A e B exercem somente as componentes e da força sobre o eixo.
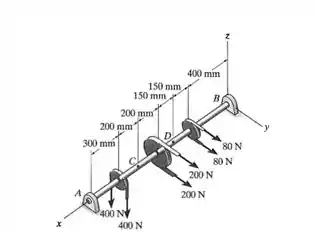
Passo 1
Primeiro, vamos fazer o diagrama do corpo livre
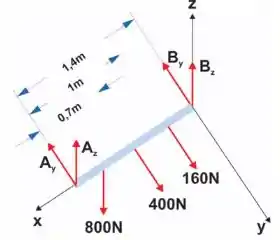
Passo 2
Vamos usar as equações de momento para e para encontrar e .
Passo 3
Por fim, vamos analisar o segmento
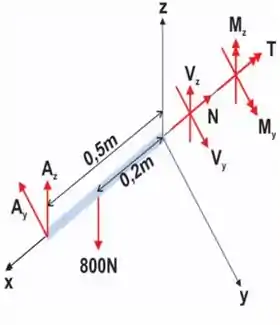
Passo 4
E usar as equações de equilíbrio e momento para cada eixo a fim de encontrar o que foi pedido.
Resposta
Exercícios de Livros Relacionados
O esqui suporta o peso de 900N( ≈ 90k g ) do homem. Se a carga de neve em sua superfície inferior for trapezoidal, como mostra a figura, determine a intensidade w e, então, represente graficamente os
Represente graficamente os diagramas de força cortante e momento fletor para a viga.
O pino liso está apoiado em duas chapas A e B e sujeito a uma carga de compressão de 0,4k N / m provocada pela barra C . Determine a intensidade da carga distribuída w 0 das chapas agindo sobre o pino
Represente graficamente os diagramas de força cortante e momento fletor para a viga de madeira e determine a força cortante e o momento fletor em todo o comprimento da viga em função de x .
Represente graficamente os diagramas de força cortante e momento fletor para a viga.