Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 149
Uma haste esbelta de comprimento e massa está soldada na borda de um aro de raio . Se o aro é liberado a partir do repouso na posição mostrada, determine a velocidade do centro do aro, após ter dado uma volta e meia. Assuma que não há deslizamento e que existe um contato contínuo entre o aro e a sua superfície de apoio. Despreze também a massa do aro.
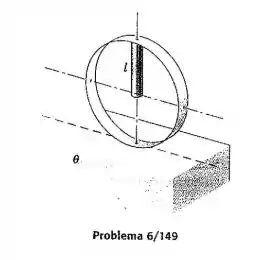
Passo 1
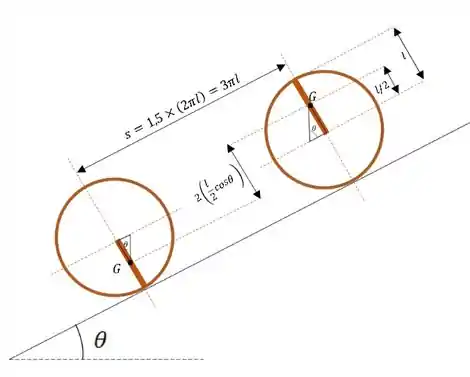
A variação da energia cinética do corpo é dada por
A variação da energia potencial, por sua vez, é dada por
Por não haver deformação elástica, o termo temos . Assim,
Pela figura, note que o deslocamento vertical é dado por
De forma que
Passo 2
Aplicando a relação Trabalho-Energia, temos que
Substituindo os valores encontrados no passo anterior, ficamos com:
Simplificando e isolando , encontramos
Resposta
Exercícios de Livros Relacionados
Um satélite de 450 kg é posto em uma órbita circular a 6.360 km acima da superfície da Terra. Nessa elevação, a aceleração da gravidade é de 2,4 m/ s 2 . Determine a energia cinética do satélite, sabe
Em uma operação de mineração, uma caçamba cheia de minério é suspensa por um guindaste móvel que se desloca lentamente ao longo de uma ponte estacionária. O guindaste desloca-se a uma velocidade de 3
Em uma operação de mineração, uma caçamba cheia de minério é suspensa por um guindaste móvel que se desloca lentamente ao longo de uma ponte estacionária. A caçamba não deverá oscilar mais que 4 m hor
Determine a máxima velocidade escalar teórica que pode ser alcançada em uma distância de 360 m por um carro inicialmente em repouso considerando que não há deslizamento. O coeficiente de atrito estáti
Um trem de metrô está viajando numa velocidade escalar de 48 km/h quando os freios são plenamente aplicados apenas nas rodas do carro A, causando então o deslizamento nos trilhos. Sabendo que o coefic