Em uma operação de mineração, uma caçamba cheia de minério é suspensa por um guindaste móvel que se desloca lentamente ao longo de uma ponte estacionária. O guindaste desloca-se a uma velocidade de m/s quando sofre uma parada repentina. Determine a distância horizontal máxima de oscilação da caçamba.

Fala aê!! Tá blz? Inicialmente, para melhor visualização da resolução deste problema, podemos considerar que o guindaste esteja se movendo com velocidade constante de m/s na situação “”, mostrada na figura abaixo, e que na situação “” houve uma parada repentina, onde a caçamba de minério passou a oscilar devido ao princípio de inércia, deslocando-se horizontalmente por uma distância “”, a qual devemos encontrar.

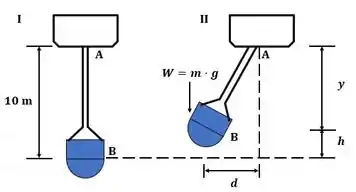
Deste modo, podemos dizer que:

Agora utilizamos o princípio de trabalho e energia, para encontrarmos o valor da altura :

Em seguida, utilizando o teorema de Pitágoras, com base na situação “” mostrada na imagem a abaixo, devemos encontrar o valor do deslocamento.

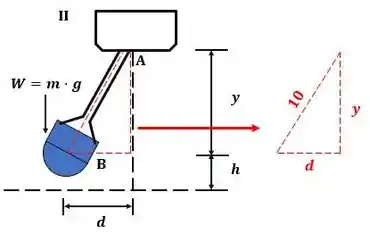
OBS: