Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 208

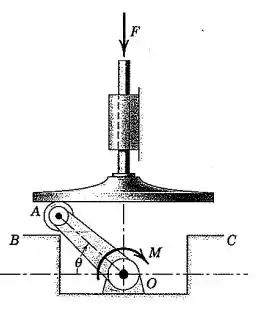
Um torque constante M ultrapassa o momento em torno de O devido à força F sobre o embolo, e resulta em uma aceleração angular θ ¨ = 100 1 - c o s θ r a d / s 2 . Se a manivela AO é liberada a partir do repouso em B, onde θ = 30 ° , e atinge o batente em C, onde θ = 150 ° , apresente graficamente a velocidade angular θ ˙ como uma função de θ e encontre o tempo t para a manivela girar de θ = 90 °   a t é   θ = 150 ° .

Passo 1

Bom pessoal, o enunciado já deu a equação da aceleração angular θ ¨ . :

θ ¨ = 100 1 - c o s θ r a d / s 2

Podemos integrar esta equação para encontrar a velocidade angular θ ˙ a partir da relação:

θ ˙ d θ ˙ = θ ¨ d θ  

O limite inferior de integração para θ ˙ é zero, pois o sistema parte do repouso. Já para θ , o enunciado nos dá que   θ = 30 ° = π 6   .   Temos então:

∫ 0 θ ˙ θ ˙ d θ ˙ = ∫ 0 θ 100 1 - c o s θ d θ

θ 2 ˙ 2 = 100 θ - s e n θ θ π / 6  

θ ˙ = 10 2 ( θ - s e n θ - 0,0236

Agora você pode usar o Software que preferir para plotar o gráfico da equação. Mas a cara dele vai ficar a seguinte:

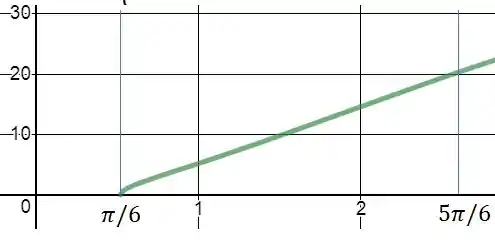
Os limites estão em radianos, mas é o que se encontra dentro das linhas azuis.

Agora, para encontrar o tempo t, basta integrar a função acima:

θ ˙ = d θ d t = 10 2 ( θ - s e n θ - 0,0236

∫ 0 t d t = ∫ π / 2 5 π / 6 d θ 10 2 ( θ - s e n θ - 0,0236

Fazendo a integração numérica, encontramos que:

t = 0,07 s

Resposta

θ ˙ = 10 2 ( θ - s e n θ - 0,0236

t = 0,07 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois satélites estão em orbitas circulares equatoriais de diferentes altitudes. O satélite A está em uma órbita geossíncrona (uma com o mesmo período que o da rotação da Terra, de modo que ele “paira”
A figura mostra as pás do impelidor de uma bomba centrífuga que gira com uma velocidade constante no sentido horário de 200 rpm. As partículas de fluido possuem uma velocidade absoluta cuja componente
Cada um dos dois carros A e B está viajando com uma velocidade constante de 72 km/h. Determine a velocidade e a aceleração do carro A como percebida por um observador se deslocando e girando com o car
Uma câmara de teste A é utilizada para estudar enjoo. A câmara é capaz de oscilar em torno de um eixo horizontal através de O de acordo com θ = θ 0 s e n 2 π f 1 t , e, ao mesmo tempo, possui um movim
Próximo do final de sua corrida para decolagem, o avião está girando (arfagem do nariz para cima) imediatamente antes de levantar voo. A velocidade e a aceleração da aeronave, expressas em termos do m