Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 140

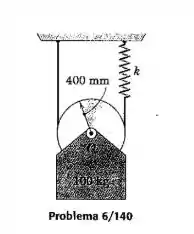
A polia com raio de 400   m m tem uma massa de 50   k g e um raio de giração de 300   m m . A polia e sua carga de 100   k g estão suspensas pelo cabo e pela mola, que possui uma rigidez de 1,5   k N / m . Se o sistema é liberado a partir do repouso com a mola inicialmente esticada de 100   m m , determine a velocidade de O após ter caído 50   m m .

Passo 1

Pela lei de conservação da energia mecânica, temos

T 1 + V g 1 + V e 1 = T 2 + V g 2 + V e 2

De forma que

∆ T + ∆ V g + ∆ V e = 0

Portanto, para achar v basta calcular cada um dos termos da equação anterior separadamente.

Passo 2

Sabemos que a energia cinética T do corpo é dada pela seguinte equação

T = 1 2 m v - 2 + 1 2 I - ω 2 ,

Onde m é a massa total do corpo (polia+carga), v - é a velocidade do centro de massa, I - o momento de inércia do corpo em relação ao seu centro de massa e ω a velocidade angular.

Dando sequência, temos

  ∆ T = 1 2 150 v 2 + 1 2 50 0,3 2   v 0,4 2

Resolvendo para   ∆ T , ficamos com

  ∆ T = 89,06 v 2

A equação para a energia potencial gravitacional é

∆ V g = m g h

Substituindo os valores, temos

∆ V g = 150 9,81 ( - 0,05 )

Assim,

∆ V g = -   73,57   J

Por fim, para a energia potencial elástica

∆ V e = 1 2 k ( x 2 - x 1 ) ²  

Logo,

∆ V e = 1 2 1500 [ 0,1 + 2 × 0,05 2 - 0,1 2 ]

Resultando em

∆ V e = 22,5   J

Passo 3

Retomando a equação do Passo 1 e substituindo valores, temos:

89,06 v 2 - 73,57 + 22,5 = 0

Resolvendo para v , temos

v ≅ 0,757 m s

Resposta

v ≅ 0,757 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um trem de metrô está viajando numa velocidade escalar de 48 km/h quando os freios são plenamente aplicados nas rodas dos carros B e C, causando então o deslizamento nos trilhos, mas não são aplicados
As caixas são transportadas por uma esteira com uma velocidade v 0 até o início de um plano inclinado fixo em A, onde elas deslizam e finalmente caem em B. Sabendo que μ = 0,40 , determine a velocidad
As caixas são transportadas por uma esteira com uma velocidade v 0 até o início de um plano inclinado fixo em A, onde elas deslizam e finalmente caem em B. Sabendo que μ k = 0,40 , determine a velocid
Os pacotes são descarregados em um declive em A com velocidade de 1 m/s. Eles deslizam ao longo da superfície ABC para a esteira transportadora que se move com velocidade de 2 m/s. Sabendo que μ k = 0
Um pacote é lançado 10 m para cima num aclive de 15 ° de forma que alcança o topo da inclinação com velocidade nula. Sabendo que o coeficiente de atrito cinético entre o pacote e a inclinação é 0,12 ,