Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 6
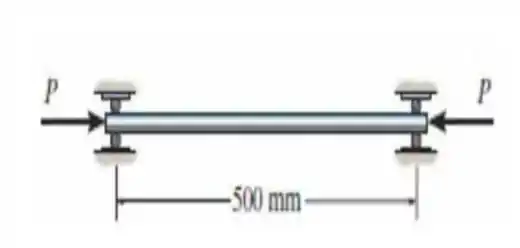
6. A haste é feita de aço. Determine, com aproximação de , o menor diâmetro da haste que suportará a carga sem flambagem. As extremidades estão apoiadas em roletes.
Passo 1
E ai? Como tá?
Bem! Como as extremidades da haste estão presas por roletes (sem reação de mometo), de cara já tiramos que o fator de comprimento efetivo da haste é igual a .
E do enunciado tiramos os seguintes dados:
Vamos seguir!
Passo 2
Vamos então, usar a fórmula da carga crítica para a flambagem:
Como a haste é cilíndrica e tem raio , o momento de inércia é dado por:
E substituindo os valores numéricos adequados, chegamos até:
Isolando :
E como o diâmetro é o dobro do raio :
Passo 3
Mas vamos refletir: esse diâmetro aguenta teoricamente essa carga, mas será que a tensão causada por essa carga não vai fazer o nosso material sair do regime linear elástico?
Agora, que já achamos o raio da seção transversal da nossa haste, e sabemos o valor da carga crítica , podemos aplicar então a velha e conhecida fórmula de tensão, dada pela divisão da força , pela área em que ela atua, para checar se tá tudo certo:
O valor da tensão crítica é menor do que a tensão admissível para o aço , que é igual a .
Então, tudo ok com nosso resultado!