Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 153
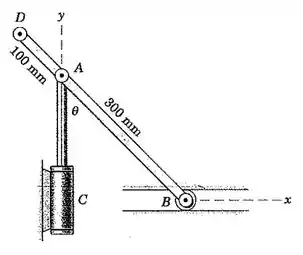
Se a haste do pistão do cilindro hidráulico C tem uma velocidade constante para cima de 0,5 /s, calcule a aceleração do ponto D para a posição que é igual a 45
Passo 1
Galera, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do que realmente importa no mecanismo. Ah, e não esquece de passar tudo que está em milímetros para metros!
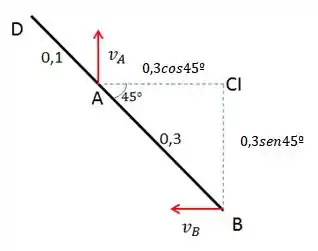
Vamos começar calculando a velocidade angular da barra. Isso pode ser feito pelo método do Centro Instantâneo , como pode ser visto pela figura.
O valor negativo para a distância acontece por que esse é um valor que é medido do até o ponto aonde estamos avaliando a velocidade. Sendo assim, aponta para a esquerda e por isso, consideramos negativo. A velocidade no ponto aponta para cima, e por isso, consideramos positivo. Fazendo isso, vamos encontrar já qual vai ser o sinal da velocidade angular!
(Você pode também fazer a regra da mão direita e vai ver que a velocidade angular do ponto em relação ao está apontando para dentro da página, sentido horário de rotação, e por isso é negativa ;) ).
Passo 2
Bom, agora vamos analisar o mecanismo. Esta etapa vai ser muito importante!! Vamos em tópicos:
-Sabemos que B está limitado ao curso do trilho, logo sua aceleração está obrigatoriamente na horizontal.
-Já o ponto A se move ao longo do pistão com velocidade constante, logo não há aceleração.
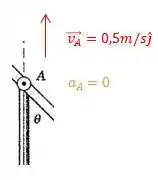
-Portanto o sistema não possui nenhuma aceleração na componente vertical. Isto limita a aceleração no ponto D na componente horizontal!
Beleza? Por isso é importante desenhar o diagrama e identificar o tipo de apoio em cada ponto!!
Passo 3
Como sabemos que a aceleração em vale , vamos usar a equação da aceleração relativa para os pontos e e assim encontrar a aceleração de ...
Onde:
Se liga que indica a distância que vai de até , portanto:
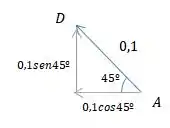
Voltando:
Se liga nas regrinhas para aplicar o produto vetorial nesses caras!
E para a aceleração tangencial temos:
Não sabemos qual o valor da aceleração angular , mas sabemos que ela vai estar apontando para dentro ou para fora da página, logo:
Substituindo e resolvendo...
Agora, vamos substituir os valores encontrados na equação da aceleração relativa, lembrando que a aceleração de certamente está no eixo horizontal e que não possui aceleração!
Decompondo nas direções, temos o sistema:
Da segunda equação temos que:
O que nos indica portanto que a aceleração angular será
Beleza, mas a questão pediu para a gente encontrar a aceleração do ponto , para isso, vamos substituir na primeira equação:
Como encontramos um valor positivo, essa aceleração aponta para a direita!