Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 150

Os componentes de uma serra mecânica alternativa são apresentados na figura. A lamina de serra é montada em um arco que desliza ao longo da guia horizontal. Se o motor fira o volante a uma velocidade constante no sentido anti-horário de 60 rpm, determine a aceleração da lamina para a posição onde θ = 90 ° , e encontre a aceleração angular correspondente da barra AB.

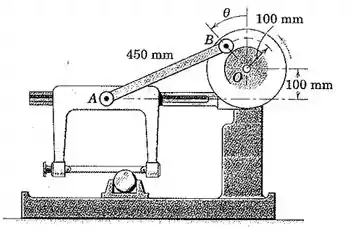
Passo 1

Galera, como já é de costume, primeiro vamos organizar todos os dados do enunciado e fazer um esboço do que realmente importa no mecanismo.

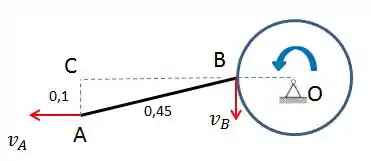
Vamos começar calculando as velocidades de A e B. A partir do volante O, nós podemos calcular a velocidade em B:

ω = 60 r p m 2 π 60 = 2 π   r a d / s

v B = ω × r = 2 π × 0,1 = - 0,63 j ^   m / s

Pela Figura, vemos ainda que o ponto C é o Centro Instantâneo de Velocidade nula. Portanto:

ω A B = v B r B C = - 0 , 63 0 , 439 = - 1,44 k ^ m s

v A = ω A B × r A C = - 1,44 k ^ × 0,1 j ^   = - 0 , 144 i ^   m / s

A partir do volante O, podemos calcular a aceleração de B:

a B = - r B O ω B O 2 + α B O × r B O = - ( 2 π ) 2 - 0 , 1 i ^ + 0

a B = 3,95 i ^ m / s 2

Agora em relação à aceleração de A, é importante notar que ela está limitada pela movimentação do curso da serra, ou seja, a A está na horizontal!!

Passo 2

Neste passo, vamos usar a equação da aceleração relativa para os pontos A e B.

a B = a A + a B / A n + a B / A t

Onde:

a B / A n = ω A B × ω A B × r B / A = - - 1,44 2 0,439 i ^ + 0 , 1 j ^ = - 0 , 91 i ^ - 0 , 21 j ^   m / s 2

a B / A t = α A B × r B / A = α A B - 0 , 1 i ^ + 0 , 439 j ^ m / s 2

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

3,95 i ^ = a A i ^ - 0,91 i ^ - 0,21 j ^ + α A B - 0,1 i ^ + 0,439 j ^

Decompondo nas direções, temos o sistema:

3,95 i ^ = a A i ^ - 0,91 i ^ + α A B - 0,1 i ^

0 = - 0,21 j ^ + α A B 0,439 j ^

Resolvendo o sistema, temos:

α A B = 0,478   k ^   r a d / s 2

a A = 4,908 i ^   m / s 2

Resposta

α A B = 0,478   k ^   r a d / s 2

a A = 4,908 i ^   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na posição mostrada, a haste fina se move a uma velocidade constante u = 3 in./s para fora do tubo BC. Ao mesmo tempo, o tubo BC gira a uma taxa constante ω 2 = 1.5 r a d / s em relação ao braço CD. S
Na posição mostrada, a haste fina se move a uma velocidade constante u = 3 pol./s para fora do tubo BC. Ao mesmo tempo, o tubo BC gira a uma taxa constante de ω 2 = 1.5r a d/ s em relação ao braço CD.
Dois discos, cada um com raio de 130 mm, são soldados à haste CD de 500 mm. A unidade de haste e discos gira a uma taxa constante ω 2 = 3 r a d / s em relação ao braço AB. Sabendo que no instante most
No problema 15.244, determine a velocidade e aceleração do (a) Ponto G, (b) Ponto H15.244 Dois discos, cada um com raio de 130 mm, são soldados à haste CD de 500 mm. A unidade de haste e discos gira a
A placa vertical mostrada é soldada ao braço EFG e toda a unidade gira a uma taxa constante ω 1 = 1.6 r a d / s em torno do eixo Y. Ao mesmo tempo, uma correia de elos contínua se move ao redor do per