Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 22

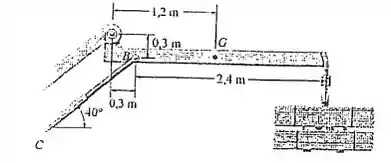
A lança do guindaste articulado tem um peso de 625 N e centro de gravidade em G. Se ele suporta uma carga de 3000 N, determine a força que age no pino A e a força no cilindro hidráulico BC quando a lança está na posição mostrada

Passo 1

Macete da questão : A é um pino. Isso quer dizer que suporta força de todas as direções. Ou seja, teremos forças e

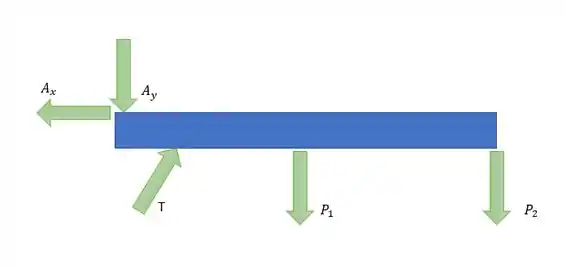
Temos Também o braço BC que faz uma força T na direção que que esta apoiado. No nosso caso, angulado em 40 º. E dois pesos do lado direito. Vamos ver o diagrama de forças

Passo 2

Bem estamos em equilíbrio então As forças verticais, horizontais e Momentos binários se anulam

Vamos definir uma Orientação antes de começar. Gosto sempre de trabalhar em sentido horário. Essa orientação é arbitrária, se você estiver feito no sentido contrário, beleza! Só ao conferir as contas os sinais estarão trocados.

Então vamos lá. Tudo o que fizer meu sistema tentar rodar em Horário é ( + ), tudo o que tentar fazer tentar rodar em sentido contrário é ( - ) .

Outra coisa. Quando fazemos momento Binário temos que olhar para o PAR distância e força. Elas têm que ser ortogonais. Isso quer dizer que se uma força é horizontal ela faz par com distância na vertical. E vice-versa. Show! Vamos cair dentro.

Passo 3

Se olharmos para o momento binário partindo do ponto A. Vemos que e tentam fazer o sistema rodar no sentido horário. Enquanto T tenta fazer o sistema rodar no sentido anti-horario. Logo teremos a seguinte equação

Passo 4

Vamos olhar agora para as reações verticais

Agora as reações em X

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3.38. O peso de 5k g é suportado pela corda AC, pelo rolete, e por uma mola. Se a mola possui um comprimento não deformado de 200m m . Determine a distância d até onde o peso está localizado quando em

3.42. Determine a massa de cada um dos dois cilindros se eles causam um deslocamento s = 0,5m quando suspensos pelos anéis em A e B. Observe que s = 0 quando os cilindros são removidos.

3.31. As molas no arranjo de cabos estão originalmente deformadas em 0,3m quando θ = 0 . Determine a força vertical F que deve ser aplicada, de modo que θ = 30 ° .

3.32. Determine a intensidade e a direção θ da força de equilíbrio F A B exercida ao longo da barra AB pelo aparato de tração mostrado. A massa suspensa é de 10k g . Despreze a dimensão da polia em A.

5.40. A plataforma possui um peso de 1,25k N e centro de gravidade em G 1 . Se ela deve suportar uma carga máxima de 2k N colocada no ponto G 2 , determine o menor contrapeso W que deve ser colocado e