Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 32
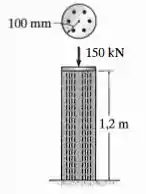
A coluna é construída de concreto de alta resistência e seis hastes de reforço de aço . Se for submetida a uma força axial de , determine o diâmetro exigido para cada haste, de modo que da carga seja suportada pelo concreto e , pelo aço.
Passo 1
Fala aí pessoal, tudo certo? Nossa meta aqui é encontrar os diâmetros de cada haste de aço, uma fórmula que relaciona a área do material com o esforço resistido é a fórmula do deslocamento, a gente vai usar ela pra encontrar a área do aço e enfim o diâmetro de cada haste, ok?
Bacana, mas como isso me ajuda? Bom os materiais precisam trabalhar em perfeita aderência, já pensou se o aço deformasse mais ou menos que o concreto? Então quando a gente aplica uma carga, mesmo que cada material resista a uma parcela diferente, eles precisam ter o mesmo deslocamento. Com isso temos a equação de compatibilidade:
Legal, temos uma relação entre os dois materiais. O enunciado também nos disse a parcela da carga que cada material resistia, sendo assim a gente pode já calcular aqui já que serão super necessárias pra resolver a questão.
O concreto resiste a 1/4 da carga.
Para as hastes de aço, as relações de carga-carregamento devem ser de .
Passo 2
Bom definido nosso objetivo bora partir pra equação de compatibilidade dos deslocamentos.
Lembrando que:
Então a gente vai ter:
Beleza, mas quem é cada parâmetro aí?
As forças foram calculadas no passo 1, e são uma parcela da carga total.
O módulo de elasticidade do aço A-36 como indicado, pode ser encontrado nas tabelas do livro e tem valor:
O módulo de elasticidade do concreto não nos foi informado, sendo assim pode se adotar um valor genérico pois existem várias classes de concreto. Aqui adotaremos:
E por fim as áreas, e repare que aqui a área do concreto vai ser dada por:
E a área de aço é o que a gente e vamos deixa-la como incógnita para no fim isolarmos o diâmetro, beleza?
Passo 3
Voltando a equação de compatibilidade, a gente pode substituir todo mundo e como o comprimento L é igual para ambos os materiais a gente pode dividir os dois lados da equação por L para eliminá-lo das nossas continhas.
E para encontrar uma relação com a área de aço, a gente pode rearrumar a continha dessa forma.
Substituindo toda nossa galera.
E a gente pode passar esse valor dividindo a área de aço, e enfim conseguiremos isolar.
E assim a gente tem:
Como são 6 hastes, a gente precisa dividir por 6 para achar a área de cada haste.
E como a área de uma seção circular é dada por:
A gente pode dizer que:
Substituindo:
Enfim conseguimos.