Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas de Revisão - Ex. 131

As hastes de aço BE e CD têm cada uma 16 mm diâmetro ( E = 200   G P a ) ; as extremidades das hastes são de rosca única com passo de 2,5 mm. Sabendo que depois de perfeitamente ajustados, a rosca C é apertada de uma volta completa, determine (a) a tração na haste CD, (b) a deflexão do ponto C do elemento rígido ABC.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine a tração na haste CD e a deflexão do ponto C do elemento rígido ABC. Para isso vamos representar o elemento com um diagrama de corpo livre, sendo θ a rotação Da barra A B C como mostrado.

Considerando que: δ B = 0,15 θ           δ C = 0,25 θ

δ C = δ t u m - P C D L C D E C D A C D

Isolando Pcd temos:

  P C D = E C D A C D L C D   x   δ t u m - δ C                                                                                                 = 200   x   10 9 P a   x   π 4   x   0,016 m 2 2 m   x   0,0025   m - 0,25 θ = 50,265   x   10 3 - 5,0265   x   10 6 θ

O alongamento é dado por:

δ B = P B E L B E E B E A B E     o u     P B E =   E B E A B E L B E P B E = 200   x   10 9 P a   x   π 4   x   0,016 m 2 3   m   x   0,15 θ = 2,0106   x   10 6 θ

Do corpo livre da seção ABC abaixo gurizada, podemos calcular o momento em A:

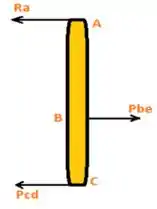
+ ∑ M A = 0 :     0,15 P B E - 0,25 P C D = 0 0,15   x   2,0106   x   10 6 - 0,25   x   ( 50,265   x   10 3 - 5,0265   x   10 6 θ = 0 θ = 8,0645   x   10 - 3 θ r a d

Passo 2

Agora sim podemos atender o que o enunciado pede :D

  1. P C D = 50,265   x   10 3 - 5,0265   x   10 6     x   8,0645   x   10 - 3 = 9,7288   x   10 3 N
  2. δ C = 0,25 θ = 0,25   x   8,0645   x   10 - 3 = 2,0161   x   10 - 3 m  

Resposta

  1. P C D = 9,73   k N
  2. δ C = 2,02   m m   ←
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver problema 148 selecionando o perfil laminado de aço de 250 mm de altura nominal
Um mergulhador de 670N salta de uma altura igual a 635mm, sobre a extremidade A de uma prancha de trampolim, de seção transversal uniforme, como mostrado. Assumindo que as pernas do mergulhador perman
Duas barras de aço maciças, cada uma com 56mm de diâmetro, são soldadas juntas para formar o suporte mostrado. Usando E = 200 GPa e G = 77 GPa, determinar a deflexão vertical do ponto A.
A viga AB é simplesmente apoiada sofre um impacto em D devido a um bloco de massa m, que se desloca horizontalmente com uma velocidade v 0 . Mostrar que a tensão normal máxima resultante σ m na viga,
A montagem ABC é feita de um aço para o qual E = 200 G P A e σ e = 320 G P a . Sabendo-se que uma energia de deformação de 5J deve ser absorvida pela montagem, assim que a carga axial P é aplicado, de