Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 6

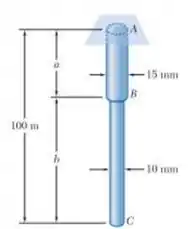
Duas hastes de latão AB e BC, de diâmetro constante, serão conectadas por brasagem em B para formar uma haste não uniforme de comprimento total igual a 100 m, que será suspensa por um apoio em A, conforme mostrado. Sabendo que a densidade do latão é 8470 kg / m³, determine (a) o comprimento da haste AB para a qual a tensão normal máxima em ABC é mínima, (b) o correspondente valor da máxima tensão normal.

Passo 1

E ai gurizada tudo belezinha??? Antes de qualquer coisa vamos determinar a área das seções :D

Sabendo que a área é calculada como:

A A B = π 4 × 15 × 10 - 3 2 = 176,71 × 10 - 6 m ²

A B C = π 4 × 1 0 × 10 - 3 2 = 78,54 × 10 - 6 m ²

O comprimento b é dada por:

b = 100 - a

Para calcularmos o peso da haste levando em consideração a densidade fornecida no enunciado para ambas a seções teremos:

P A B = ρ × g × A × L

P A B = 8470 × 9,81 × 176,71 × 10 - 6 × a = 14,69 a

Para a outra seção temos

P B C = ρ × g × A × L

P B C = 8470 × 9,81 × 78,54 × 10 - 6 × 100 - a = 652,59 - 6,52 a

Passo 2

Agora podemos calcular a tensão nos pontos A e B, venham comigo :D

σ = P A A B = P A B + P B C A A B

σ A = 652,59 - 6,52 a + 14,69 a 176,71 × 10 - 6 = 3,69 × 10 6 + 46,16 × 10 3 a

Agora para B tem-se:

σ = P A B C = P B C A B C

σ B = 652,59 - 6,52 a 78,54 × 10 - 6 = 8,3 × 10 6 - 83,1   × 10 3 a

Passo 3

Para calcularmos o comprimento da haste AB para a qual a tensão normal máxima em ABC é mínima, temos que igualar as equações das tensões do passo 2, partiu!!!

3,69 × 10 6 + 46,16 × 10 3 a = 8,3 × 10 6 - 83,1   × 10 3 a

Isolando a teremos:

a = 35,7   m

Passo 4

Agora gurizada, sei que estão cansados, mas já vai acabar, como encontramos o “a” no passo 3 podemos substituir nas equações das tensões do passo 2 e acabou :D

σ A = 3,69 × 10 6 + 46,16 × 10 3 a

σ B = 8,3 × 10 6 - 83,1   × 10 3 a

Substituindo a = 35,7   m

σ A = 3,69 × 10 6 + 46,16 × 10 3 × 35,7 = 5,33 × 10 6 P a   o u   5,33 M P a  

σ B = 8,3 × 10 6 - 83,1   × 10 3 × 35,7 = 5,33 × 10 6 P a   o u   5,33 M P a

Resposta

  1. 35,7   m
  2. 5,33 M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) para P = 13k i p sed = 1 2 i n . , determine a tensão máxima na placa mostrada, (b) resolva a parte a, supondo que não seja feito o furo em A.
Sabendo que P = 38 k N , determine a tensão máxima quando (a) r = 10 m , (b) r = 16 m m e (c) r = 18 m m .
Sabendo que o furo tem um diâmetro de 9,53 mm, determine (a) o raio r opara os quais ocorre a mesma tensão máxima no furo A e nos adoçamentos e (b) a força P correspondente máxima admissível se a tens
Sabendo que, para a placa mostrada, a tensão admissível é de 125 MPa. Determine o valor máximo admissível para P quando ar = 12m mebr = 18 m m .
Para P = 100k N , determine a espessura t mínima necessária para a placa se a tensão admissível for de 125M P a .