Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 82

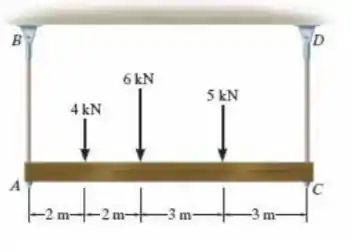
As hastes e são feitas de aço cuja tensão de ruptura por tração é . Usando um fator de segurança para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em e .

Passo 1

Falaaa! Para começar, a gente precisa calcular as forças nas hastes e para isso vamos precisar das reações de apoio. Podemos usar as equações de equilíbrio:

Adotando o sentido anti-horário vamos obter

Daí:

Como :

Passo 2

Agora pensa comigo: a tensão normal média em uma haste é dada por

Como ela tem seção circular

Mas a máxima tensão que essa haste aguenta é

Porém, queremos usar um fator de segurança de para essa tensão normal. O que isso quer dizer? Cara, quer dizer que, na verdade, a nossa tensão máxima permitida é DIVIDIDO pelo fator de segurança

Já que essa é a tensão máxima que nossa haste pode suportar, podemos igualar esse valor a tensão média na haste, para achar o valor do diâmetro da barra para essa situação limite:

Temos

Passo 3

Olha que lindo, a gente achou uma expressão para o diâmetro de uma haste com as características físicas iguais as das nossas hastes. O que fazemos? A gente substitui os valores para o caso da haste e para a haste :

- Para

Resposta

Para :

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas forças são aplicadas como mostrado na barra AB, que é soldada ao cilindro DE, de diâmetro 50mm. Considerando que todas as tensões permanecem abaixo do limite de proporcionalidade, determinar as t

Determinar os planos principais e as tensões principais para o estado plano de tensões, resultante da superposição dos dois estados planos de tensões mostrado.

Um tubo de aço de 300 mm de diâmetro externo é fabricado com chapa fina de 6,35 mm de espessura, soldada ao longo de uma hélice que forma um ângulo de 22,5° com um plano perpendicular ao eixo do tubo.

Três forças são aplicadas, como mostrado, a uma viga em balanço. Determinar as máximas tensões de cisalhamento e as orientações nos pontos H e K.

No eixo de um automóvel atuam as forças e o torque mostrado. Sabendo-se que o diâmetro do eixo é de 30 mm, determinar os planos principais e as tensões principais no ponto H, localizado no cume da sup