Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 88
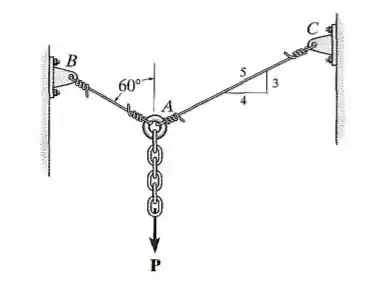
Os dois cabos de aço e são usados para suportar a carga. Se ambos tiverem uma tensão de tração admissível , determine o diâmetro exigido para cada cabo se a carga aplicar for .
Passo 1
Para encontrarmos o que queremos vamos fazer o somatório das forças:
Resolvendo esse sistema de equações vamos obter
Passo 2
Lembrando que a tensão normal admissível (calculada da mesma forma que a tensão normal média) é dada por
Para o fio AB:
Para o fio AC:
Resposta
Para o fio AB:
Para o fio AC:
Exercícios de Livros Relacionados
O pino está submetido a cisalhamento duplo, visto que é usado para interligar os três elos. Devido ao desgaste, a carga é distribuída nas partes superior e inferior do pino como mostra o diagrama de c
Para um estado plano de tensões é conhecido que as tensões, normal e de cisalhamento, são dirigidas como indicado e que σ x = 30M P a , σ y = 80M P a e σ m á x = 120M P a á . Determinar: (a) a orienta
Para o elemento mostrado, determinar a variação τ x y para que a máxima tensão de tração seja igual ou inferior que 75M P a .
Para um estado plano de tensões é conhecido que as tensões, normal e de cisalhamento, são dirigidas como indicado e que σ x = 90M P a , σ y = 45M P a e σ m í n = 30M P a í . Determinar: (a) a orientaç
Para o elemento mostrado, determinar a variação τ x y para que a máxima tensão de cisalhamento seja igual ou inferior que 140M P a .