Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 84

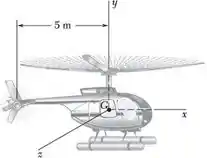
No helicóptero mostrado na figura, um rotor de cauda é usado para impedir a rotação da cabine à medida que a velocidade das pás principais é alterada. Admitindo que o rotor de cauda não esteja em operação, determine a velocidade angular final da cabine após a velocidade das pás principais ter sido alterada de 180 para 240 rpm. (A velocidade das pás principais é medida em relação à cabine, que tem um momento de inércia centroidal de 1.000 kg ∙ m2. Cada uma das quatro pás principais é considerada como uma barra delgada de 4,2 m de comprimento e 25 kg de massa.)

Passo 1

Seja Ω a velocidade angular da cabine e ω a velocidade angular das pás em relação à cabine. A velocidade angular absoluta das lâminas é Ω + ω .

ω 1 = 180   r p m = 6 π   r a d / s

ω 2 = 240   r p m = 8 π   r a d / s

Momentos de inércia.

Cabine:

I C = 650   l b ∙ f t ∙ s 2

Pás:

I B = 4 1 3 m L 2 = 4 1 3 55 32.2 14 2 = 446.38   650   l b ∙ f t ∙ s 2

Passo 2

Assuma Ω 1 = 0 .

Conservação do momento angular sobre o eixo.

I B ω 1 + Ω 1 + I C Ω 1 = I B ω 2 + Ω 2 + I C Ω 2

Ω 2 = I B ω 2 - ω 1 I C + I B = - 446.38 8 π - 6 π 446.38 + 650 = - 2.5581   r a d / s

Resposta

Ω 2 = - 24.4   r p m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola bate no chão em A com uma velocidade v 0 de 16m / s a um ângulo de 60 ° com a horizontal. Sabendo que e = 0,6 entre a bola e o chão e que após o rebote a bola alcança o ponto B com uma veloci
O pino B de 100 g desliza ao longo da fenda no braço rotativo OC e ao longo da fenda DE, que é cortada em uma placa horizontal fixa. Negligenciando o atrito e sabendo que a haste OC gira a uma taxa co
Um volante de 2.000 kg com raio de giração de 700 mm é deixadolivre a partir de uma velocidade angular de 450 rpm. Sabendo que oatrito cinético produz um binário de intensidade de 16 N m, determine o
Dois discos de mesma espessura e mesmo material são presos a um eixo como mostrado na figura. O disco A de 3 kg tem um raio rA 100 mm e o disco B tem um raio r B 125 mm. Sabendo que a velocidade angul
No Problema 17.60, determine o tempo necessário para a velocidadedo volante ser reduzida a 40 rpm no sentido horário.