Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 15
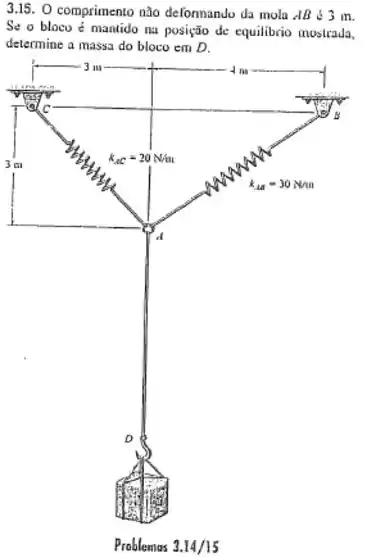
O comprimento não deformado da mola é . Se o bloco é mantido na posição de equilíbrio mostrada, determine a massa do bloco em .
Passo 1
Fala! Vamos entender o que houve. Temos uma caixa de peso . E ela é segurada por duas molas. Queremos achar a massa da caixa.
Primeira coisa é nesse tipo de questão é fazer o diagrama de corpo livre. Vamos olhar para . O lado pode ser achado por pitagoras. Ele vale . Temos então um triângulo 3/4/5. Por isso a gente pode colocar aquele triângulozinho indicando essa orientação na força .
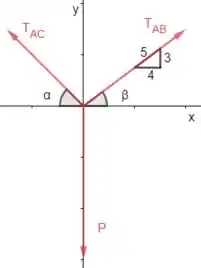
Usando as relações trigonométricas podemos descobrir os valres de
Para o ângulo como a gente tem esse triângulo 3/4/5 é mais jogo só achar o valor de seno, cosseno e tangente, porque esse não vai ser inteiro.
Para o ângulo é mais jogo achar o ângulo mesmo. Repara
Temos nessa situação forças coplanares. Como tudo deve estar em equilíbrio, o somatório de forças zera nos dois eixos. Vamos então calcular esse somatório no ponto e achar . Bora!
Passo 2
A soma de forças em e em deve ser zero.
Vamos decompor primeiro as forças em :
Nós já sabemos o valor dos cossenos:
O valor de pode ser calculado, ele é igual a força elástica da mola
Nós sabemos a mola AB não deformada tem um tamanho igual a . Nós sabemos que o triângulo que essa mola forma com a horizontal e a vertical é um triângulo retângulo 3, 4, 5, então o tamanho da mola deformada é de , ou seja ela está deformada:
Continuando nossa equação:
E cê pode pensar: Por que não achamos pela fórmula da força elástica também? Ali tem uma mola, né? Cara, é porque o enunciado não nos deu o comprimento sem deformação de . Aì não tem como descobrir sua deformação.
Passo 3
Agora vamos decompor as forças em :
O peso é igual a massa vezes a gravidade:
Como já temos os valores de e de :
Isolando :