Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 14
Passo 1
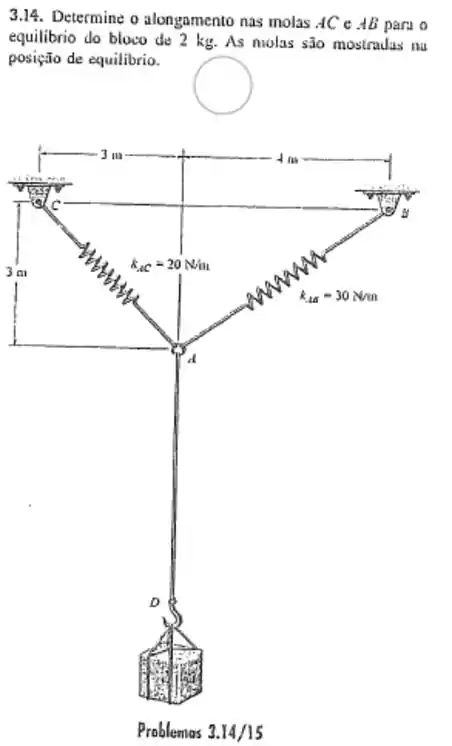
Vamos fazer o diagrama de corpo livre no ponto O:
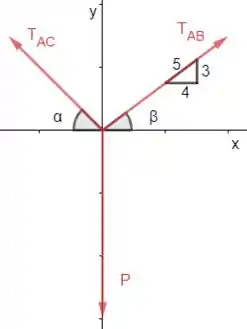
Usando as relações trigonométricas podemos descobrir os valres de
Para o ângulo :
Para o ângulo :
Passo 2
A soma de forças em e em deve ser zero.
Vamos decompor primeiro as forças em :
Nós já sabemos o valor dos cossenos:
Passo 3
Agora vamos decompor as forças em :
O peso é igual a massa vezes a gravidade:
Como já temos os valores de e de :
A tração AC é a força elástica da mola, as forças elásticas são da forma:
Então essa mola se deforma:
Passo 4
Usando a equação que encontramos no Passo 2 vamos descobrir a tração no cabo AB é:
No Passo 3, encontramos a tração em AC:
A tração em AB é igual a força elástica da mola:
Resposta
Exercícios de Livros Relacionados
Determine as forças nos cabos AB e AC necessárias para suportar o semáforo de 12 kg.Fonte: Estática Mecânica para Engenharia – 14ª ed
A carga tem uma massa de 15 kg e é elevada pelo sistema de polias mostrado na figura. Determine a força F na corda em função do ângulo θ . Desenhe a função da intensidade F contra o ângulo θ para 0 ≤
Determine as distâncias x e y para que haja equilíbrio se F 1 = 800NeF 2 = 1000N .Fonte: Estática Mecânica para Engenharia – 14ª ed