Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 16
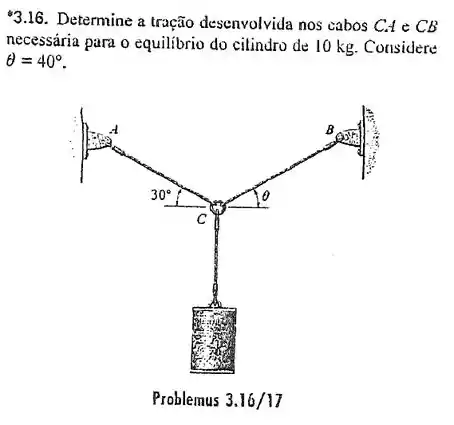
Passo 1
Vamos fazer o diagrama de corpo livre na argola C:
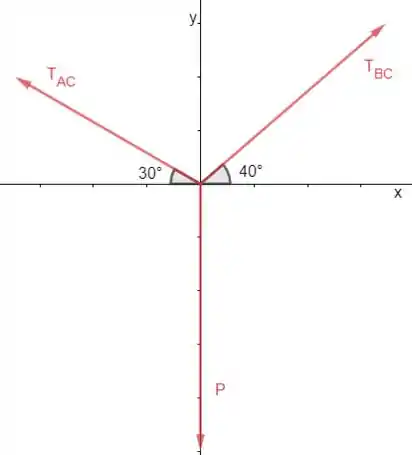
Passo 2
A soma de forças em e em deve ser zero.
Vamos decompor primeiro as forças em :
Passo 3
Agora vamos decompor as forças em :
O peso é igual a massa vezes a gravidade:
O enuncido nos dá a massa:
Usando a relação entre e que encontramos no Passo anterior
Passo 4
Usando a relação do Passo 2, vamos ter que:
Resposta
Exercícios de Livros Relacionados
22. Uma força P é aplicada em uma haste dobrada que é apoiada por um rolete e um suporte com pino. Para cada um dos três casos mostrados, determine as forças internas no ponto J :
23. Uma haste de peso W e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto J quando θ = 60 ° .
24. Uma haste de peso W e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto J quando θ = 15 0 ° .
26. Uma haste de um quarto de círculo de peso W e seção transversal uniforme é apoiada tal como mostra a figura. Determine o momento fletor no ponto J quando θ = 30 ° .
27. Para a haste do problema 7.25 , determine a intensidade e a localização do momento fletor máximo: