Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 1

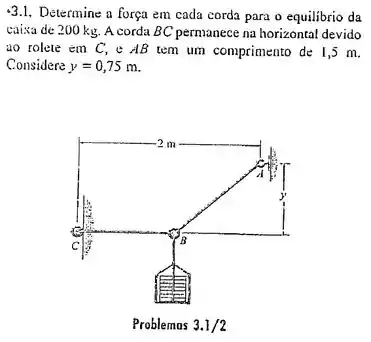
Determine a força em cada corda para o equilíbrio da caixa de 200   k g . A corda B C permanece na horizontal devido ao rolete em C , e A B tem comprimento de 1,5   m . Considere y = 0,75 m.

Passo 1

Cara, e aí? Queremos as forças nos cabos.

Primeira coisa a fazer nesses exercícios é fazer o diagrama de corpo livre. Vamos fazer para a argola B :

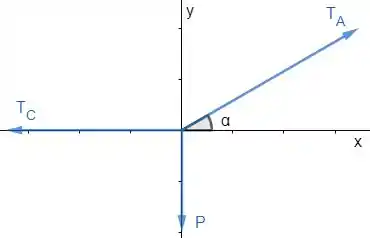
Onde P é o peso da caixa. E os T ' s são as forças nas cordas.

O valor de α pode ser encontrado através de relações trigonométricas, nós sabemos o tamanho do cateto oposto, y , e o tamanho da hipotenusa, A B (dada pelo enunciado), então podemos usar o seno:

s e n o = c a t e t o   o p o s t o h i p o t e n u s a

sen ⁡ α = y A B

sen ⁡ α = 0,75 1,5

sen ⁡ α = 0,5

α = 30 °

Bele? Percebe que a gente só tem forças coplanares. Então a gente pode usar as equações de equilíbrio em B , para x e y .

Passo 2

Como tudo isso ai tem que estar parado (em equilíbrio), a soma de forças em x e em y deve ser zero.

Vamos decompor as forças em y :

∑ F y = 0

T a sen ⁡ α - P = 0

Como y é oposto a α (ânguo que orienta T a ), a gente colocou seno ali. Lembrando que P é massa vezes gravidade

T a sen ⁡ α - m g = 0

T a sen ⁡ α = m g

T a = m g sen ⁡ α

Temos os valores de m e α , e podemos supor g = 9,81   m / s 2 . Substituindo vamos ter que:

T a = 200 9,81 sen ⁡ 30 °

T a = 3924   N

Arrendondando

T a = 3,92 × 10 3   N = 3,92   k N

Essa é a tração na corda AB.

Passo 3

Agora vamos decompor as forças em x e montar a e equação para esse eixo:

∑ F x = 0

T a cos ⁡ α - T c = 0

T c = T a cos ⁡ α

Nós sabemos o valor de T a e do ângulo α , então é só substituir:

T c = 3924 ⋅ cos ⁡ 30 °

T c = 3398   N

Arrendondando

T c = 3,40   × 10 3 = 3,40   k N

Resposta

T a = 3,92   k N

T c = 3,40   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A haste C D está presa ao colar D e passa por um colar soldado na extremidade B da alavanca A B . Desprezando o efeito do atrito, determine o binário M necessário para manter o sistema em equilíbrio q
Dois cilindros hidráulicos controlam a posição do braço robótico A B C . Na posição mostrada na figura os cilindros estão paralelos e ambos em tração. Sabendo que F a e = 600 NeF d g = 50 N . Determin
Um trilho de ferrovia de comprimento 12 m e peso 650N / m é elevado pela tenaz mostrada na figura. Determine as forças exercidas em DeF na garra B D F .
Uma tora de madeira pesando 3600 N é presa por uma tenaz como mostrado na figura. Determine as forças exercidas em E e F na garra D E F .
A tenaz mostrada na figura é usada para aplicar uma força total para cima de 45 k N no tampão da tubulação. Determine as forças exercidas em D e F na garra A D F .