Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 68

Calcule as coordenadas do centro de massa do molde metálico fundido mostrado.

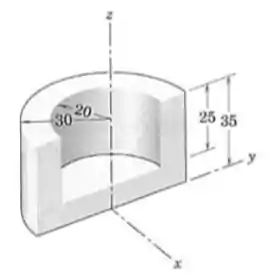
Passo 1

Então galera, questão simples, mas pode ter confusão na hora de montar a tabelinha... mas vamo com calma! Primeiro, temos que ter em mente que os centroides são dados por:

X - =   ∑ x - A   ∑ A    

  Y - =   ∑ y - A   ∑ A    

Z - =   ∑ z - A   ∑ A    

Passo 2

Agora, vamos dividir nosso problema em volumes, e a partir dai jogar na nossa formula, substituindo área por volume! A seguir uma vista aérea da figura pra vocês terem uma ideia melhor do que ta rolando!

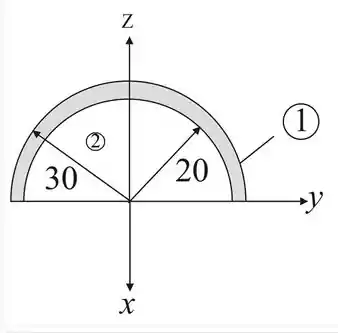
Por inspeção sabemos que o nosso sólido é simétrico em y, logo o centro de massa dele em Y é igual a 0.

Passo 3

Vamos calcular o nosso centro de massa no volume 1:

V t o t a l 1 = π 2 30 2 35 = 49500   m m 3

x - 1 = - 4 30 3 π =   - 12.73   m m

z - 1 = 17.5   m m

Vamos calcular o nosso centro de massa no volume 2:

V t o t a l 2 = - π 2 2 0 2 2 5 = - 15   710   m m 3

x - 1 = - 4 2 0 3 π =   - 8.49   m m

z - 1 = 1 2 10 + 35 = 22.5   m m

Passo 4

Agora vamos jogar na nossa formula e matar a questão de vez!!

X - =   ∑ x - V   ∑ V = 49500 - 12.73 - 15710 - 8.49   49500 - 15710 =   - 14.71   m m

Z - =   ∑ z - V   ∑ V = 49500 17.5 - 15710   22.5 49500 - 15710 = 15.17   m m

Resposta

X - =   - 14.71   m m

Y - = 0   m m

Z - = 15.17   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O quadro de ajuste da braçadeira de deslocamento especial suporte uma compressão de 500 N. Calcule a força cortante V, a tensão T e o momento fletor M na seção A da barra de braçadeira para x = 250 mm
Derive expressões para a força cortante V e o momento fletor M como funções de x na viga cantilever carregada como mostrado.
Desenhe os diagramas de cortante e momento para a viga de Prob. 5/116 repetido aqui e especifique o cisalhamento V e o momento M no comprimento médio da viga.
Desenhe os diagramas de cortante e momento para a viga carregada e especifique o cortante V e o momento M em uma seção 3 m à esquerda do suporte em A.
A viga suporta uma carga unitária uniforme w. Determine a localização x dos dois apoios de forma a minimizar o momento Mmax fletor máximo na viga. Especifique Mmax.