Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 62
A vista de topo de uma porta giratória é mostrada. Duas pessoas se aproximam simultaneamente da porta e exercem forças de módulo igual, como mostrado. Se o momento resultante em relação ao eixo de rotação da porta em vale , determine o módulo da força .
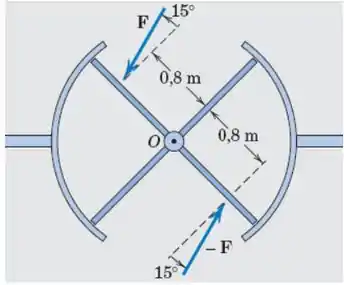
Passo 1
Vamos encontrar uma expressão para o momento de cada uma dessas forças em relação ao ponto , utilizando a seguinte fórmula
Onde é a componente da força na direção perpendicular a linha que une o ponto de ação da força e o ponto
Olhando para o triângulo formado pela força, vemos que está colado ao ângulo de e por isso é dada por
E a distância de cada uma das forças até o ponto é
Passo 2
Como as duas forças favorecem a rotação no mesmo sentido, podemos somar os momentos associados a cada uma delas para encontrar o momento resultante, que será dado por
E a ideia é que o momento seja igual a então
Pronto, tá resolvido nosso exercício pois descobrimos que precisa valer .