Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 65
Determine as coordenadas x e y do centroide da área sombreada.
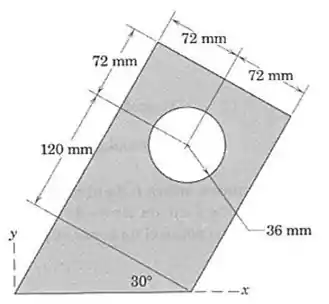
Passo 1
Então galera, questão simples, mas pode ter confusão na hora de montar a tabelinha... mas vamo com calma! Primeiro, temos que ter em mente que os centroides são dados por:
Vamos só alterar para um conjunto de coordenadas novo, para ajustarmos os cálculos e ficar mais fácil pra gente!
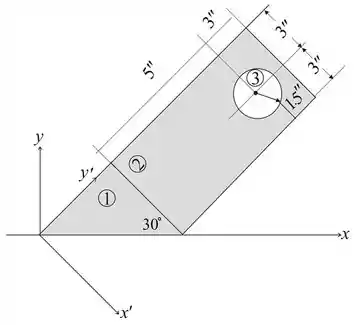
Para fazer essa conversão, vamos dizer que:
Passo 2
Agora, vamos dividir nosso problema em áreas, e a partir daí montar uma tabela pra nos auxiliar na organização dos elementos!
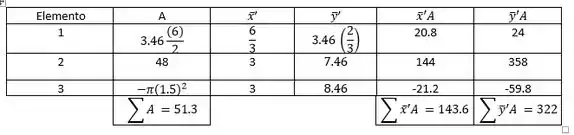
Passo 3
Agora vamos matar a questão de vez, bastando jogar na nossa fórmula
Logo,
Resposta
Exercícios de Livros Relacionados
Desenhe os diagramas de cisalhamento e momento para a viga carregada uniformemente e encontre o momento fletor máximo Mmax
Construa os diagramas de cortante e momento para a viga carregada pela força de 2 kN e o par de 1,6 kN⋅m. Indique o valor do momento fletor no ponto B.
A força de cisalhamento em libras em uma determinada viga é dada por V = 2200x-40x³, onde x é a distância em pés medida ao longo da viga. Determine a variação correspondente com x da carga normal w em
Desenhe os diagramas de cortante e momento para a viga carregada e determine o valor máximo M_max do momento.
Desenhe os diagramas de cisalhamento e momento para a viga cantilever carregada onde o acoplamento final M_1 é ajustado de modo a produzir o momento zero na extremidade fixa da viga. Encontre o moment