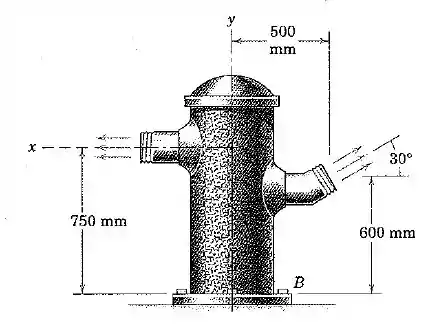
O hidrante é testado sob uma alta pressão na tubulação vertical. O escoamento total de é dividido igualmente entre as duas saídas, sendo que cada uma possui uma seção transversal de . A área da seção transversal de entrada na base é . Despreze o peso do hidrante e da água no seu interior e calcule a tração , o cortante , e o momento fletor na base do tubo vertical em . A massa específica da água é . A pressão estática da água quando entra na base em é de .

Nosso primeiro objetivo é calcular a tração na base do hidrante em . Pela equação que dá a força resultante em um sistema de escoamento:

A força resultante é a soma vetorial da tração que prende o hidrante ao chão (voltada para baixo) e força associada à pressão da água:

E quando projetamos as velocidades na direção vertical ficamos com:

E então:

Em seguida queremos calcular o cortante , nesse caso só o que precisamos fazer é projetar as velocidades no eixo horizontal, ao invés do vertical como fizemos logo acima.

Vamos definir o sentido positivo como sendo horizontal para a esquerda. Como a velocidade inicial é perpendicular ao eixo horitonal, seu componente será nula nesses cálculos:

Finalmente, queremos calcular o momento fletor na base do tubo vertical. Vamos lembrar da fórmula para essa grandeza:

É interessante pensar nessa grandeza como uma espécie de “torque” produzido por cada jato d’água que jorra do tubo. Nesse caso estamos tomando a base como ponto de referência.

O momento gerado pelo jato à esquerda do desenho é:

E os momentos gerados por cada um dos componentes (horizontal e vertical) do jato à direita do desenho são:

E então o momento total é:

Resolvido!