Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 50
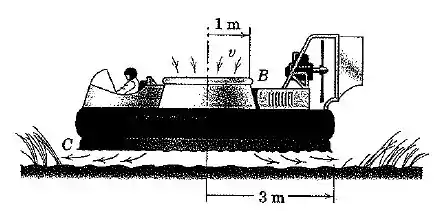
O hovercraft experimental tem uma massa total de . Ele paira junto ao solo pelo bombeamento de ar à pressão atmosférica através do duto circular de admissão em e descarrega horizontalmente sob a periferia da saia . Para uma velocidade de admissão de , calcule a pressão média do ar sob o equipamento com de diâmetro no nível do solo. A massa específica do ar é .
Passo 1
Vamos começar calculando as áreas da entrada e da saída do ar:
E podemos calcular a taxa de escoamento de massa olhando para a duto de admissão (já que temos a velocidade nesse ponto):
Passo 2
Beleza, agora vamos lembrar da equação que dá a força resultante em um sistema de escoamento:
Como o sistema acelera o ar a partir do “repouso” até uma velocidade , a variação da velocidade é:
E então a força agindo sobre o ar para acelerá-lo é:
Mas nosso objetivo é calcular a pressão do ar sob a máquina. A força associada a essa pressão tem que cumprir dois papéis: gerar a força que acabamos de calcular, e sustentar o peso da máquina. Então:
Resposta
A pressão necessária é .