Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 36

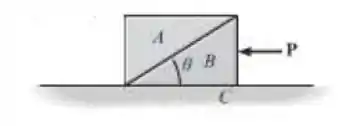
Cada um dos blocos A e B tem massa m. Determine a maior força horizontal P que pode ser aplicada a B de maneira que A não se desloque em relação a B. Todas as superfícies são lisas.

Passo 1

Se ambos os blocos não se deslocam entre si, significa dizer que a aceleração dos dois são iguais entre si! Portanto, basta resolvermos as questões de destruição de forças do nosso problema. Logo, se torna essencial fazer um diagrama de corpo livre bem feito!

Passo 2

Começaremos esboçando o diagrama de corpo livre para o nosso bloco A. Temos então:

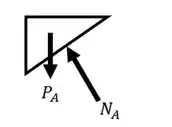
O mesmo possui uma aceleração para a esquerda dada por . Fazendo o somatório das forças, temos:

Já na direção do eixo , teremos:

Descobrimos a aceleração dos dois corpos para que não haja este deslizamento.

Passo 3

Repetiremos a mesma análise do Passo 2, só que agora para o bloco B.

Esboçando o seu diagrama de corpo livre, temos:

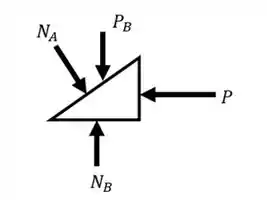
Fazendo o somatório das forças na direção do eixo , teremos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula é liberada do repouso y = 0 e cai sob a influência da gravidade e da resistência do ar. Determine o relacionamento entre v , e a distância de queda y , quando a resistência do ar for igu

Descreva como determinar se um equilíbrio é estável ou instável de acordo com d2U/dx2.

Duas estrelas ligadas gravitacionalmente com massas diferentes m1 e m2, separadas por uma distância d, giram ao redor do seu centro de massa em órbitas circulares. Demonstre que o período τ é proporci

A velocidade de uma partícula de massa m varia com a distância x conforme v(x) = ax-n. Suponha v(x = 0) = 0 em t = 0.Determine a força F(x) responsável.Determine x(t).E F(t).

Resolva o Exemplo 2.12 utilizando forças em vez de energia. Como é possível determinar se o equilíbrio do sistema é estável ou instável?