Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 32
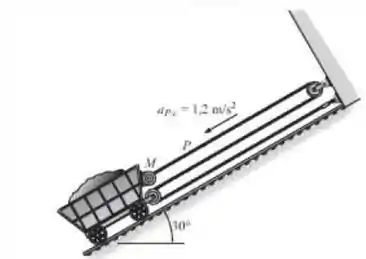
O motor M enrola o cabo com uma aceleração de , medida em relação ao carrinho de mineração de . Determine a aceleração do carrinho e a tração no cabo. Despreze as massas das polias.
Passo 1
Temos um problema que envolve polia! Começaremos analisando a cinética do problema, esboçando o diagrama de corpo livre do nosso carrinho, para despois partirmos para a parte de cinemática, relacionando as acelerações do carrinho com a da corda para que possamos resolver o nosso problema! Temos que tomar muito cuidado nesta última etapa!!!
Passo 2
Começaremos esboçando o diagrama de corpo livre dos nossos blocos. Ambos os blocos possuem um diagrama bastante semelhante, mudando apenas o valor da componente do peso. Sendo assim, temos:
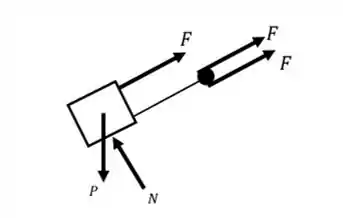
Sendo assim, ao fazermos o somatório ao longo do eixo , obteremos:
Observem que o sinal negativo da aceleração nos diz que o carrinho está descendo!
Passo 3
Devido a relação das polias, temos que a aceleração da corda e do carrinho possuem a seguinte relação:
Portanto, trabalharemos agora com acelerações relativas. Como a aceleração relativa da corda ao cabo é , temos a seguinte equação:
Mas como , temos:
Portanto, a tração no cabo é: