Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 4
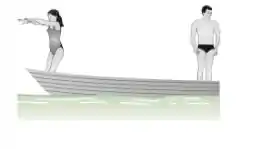
Um homem de 90 kg e uma mulher de 60 kg estão em extremidades opostas de um barco de 150 kg, prontos para mergulhar, cada um com uma velocidade de 5 m/s em relação ao barco. Determine a velocidade do barco após os dois terem mergulhado, se a mulher mergulha primeiro e se o homem mergulha primeiro.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Como foi de fim de ano?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual a velocidade para cada uma das situações. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, vamos lembrar que não existem forças externas horizontais que atuam durante os impactos, portanto o centro de massa G do sistema se move em velocidade constante.
Se alguém mergulha, a força do impulso que se pega para dar o salto faz com que o barco ande na direção contrária.
Então, vamos analisar quando a mulher pula primeiro.
Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.
Agora, o homem mergulha atrás.
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
Agora, se invertermos a ordem ali dos saltos, teremos que: