Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 10

Para o sistema de partículas do Problema 1, determine (a) o vetor de posição  do centro de massa G do sistema, (b) a quantidade de movimento linear  do sistema, (c) a quantidade de movimento angular HG do sistema em relação a G. Verifique também que as respostas encontradas para este problema e para o Problema 1 satisfazem a equação dada no Problema 2.

Problema 1

Um sistema consiste de três partículas, A, B e C. Sabemos que mA = 3 kg, mB = 4 kg e mC = 5 kg e que as velocidades das partículas, expressas em m/s são, respectivamente, vA = − 4i + 4j + 6k, vB = − 6i + 8j + 4k e vC = 2i − 6j − 4k. Determine a quantidade de movimento angular HO do sistema em relação a O.

Problema 2

Deduza a relação

entre as quantidades de movimento angulares HO e HG definidas nas equações (14.7) e (14.24), respectivamente. Os vetores  e  definem, respectivamente, a posição e a velocidade do centro de massa G do sistema de partículas em relação ao sistema de referência newtoniano Oxyz, e m representa a massa total do sistema

.

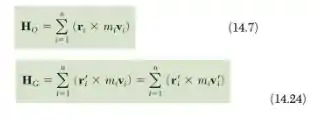
Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Como foi de fim de ano?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual o movimento angular. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, vamos lembrar que não existem forças externas horizontais que atuam durante os impactos, portanto o centro de massa G do sistema se move em velocidade constante, além de ser dado pelo vetor posição r.

Cada partícula terá o seguinte momento linear:

m A v A = 3 - 4 i + 4 j + 6 k

m B v B = 4 - 6 i + 8 j + 4 k

m C v C = 5 2 i - 6 j - 4 k

Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.

r A = 1,2   i + 1,5 k

r B = 0,9 i + 1,2 j + 1,2 k

r C = 2,4 j + 1,8 k

m A + m B + m C r = m A r A + m B r B + m c r C

r = 0,6 i + 1,4 j + 1,525 k

m v - = m A v A + m B v B + m C v C

m v - =   - 26 i + 14 j + 14 k

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

Com o segundo caso, temos que:

r A ' = r A - r -

r B ' = r B - r -

r C ' = r C - r -

H o = r A × m A v A + r B × m B v B + r C × m C v C

H o =   - 31,2   i - 64,8 j + 48 k

H G = r A ' × m A v A + r B ' × m B v B + r C ' × m C v C

H G =   - 29,45   i - 16,75 j + 3,2 k

Resposta

r = 0,6 i + 1,4 j + 1,525 k

m v - =   - 26 i + 14 j + 14 k

H o =   - 31,2   i - 64,8 j + 48 k

H G =   - 29,45   i - 16,75 j + 3,2 k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O carroAestava viajando para o leste em alta velocidade quando colidiu no pontoOcom o carroB, que estava viajando para o norte a 72 km/h. O carroC, que estava viajando para o oeste a 90 km/h, quando e
Um arqueiro demonstra sua habilidade em atingir uma bola de tênis jogada por seu assistente.Abola de tênis de 58 g tem velocidade de (10 m/s)i− (2 m/s)je está a 10 m do chão quando é atingida por uma
No Problema 1, sabendo que os destroços do pequeno avião foram encontrados no pontoA(1.200 m, 80 m) e o fragmento de 1.000 kg do helicóptero no pontoH1(400 m, −200 m), e considerando que todas as part
Em um experimento de dispersão de partículas, uma partícula alfaAé projetada com velocidadeu0= −(600 m/s)i+ (750 m/s)j− (800 m/s)kno interior de uma corrente de núcleos de átomos de oxigênio que se mo
14.25. Uma ogiva de 6 kg que se move a uma velocidade v0 (12 m/s)i (10m/s)j (400 m/s)k explode no ponto D em três fragmentos, A, B eC, que têm massa de, respectivamente, 2,5 kg, 2 kg e 1,5 kg. Sabendo