Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 231

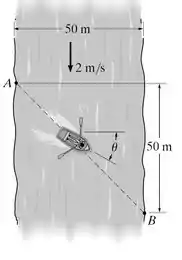
Um homem pode remar um barco a 5 m/s na água parada. Ele quer atravessar um rio de 50 m de largura até o ponto B, 50 m correnteza abaixo. Se o rio flui com uma velocidade de 2 m/s, determine a velocidade escalar do barco e o tempo necessário para fazer a travessia.

Passo 1

A velocidade escalar do barco para fazer a travessia pode ser determinada a partir da equação de velocidade relativa, sendo que para que V B / r i o = 5 cos ⁡ θ i - 5 sin ⁡ θ j   conforme o enuciado da questão.

V B =   V r i o +   V B / r i o

v b a r c o sin ⁡ 45 ° i -   v b a r c o cos ⁡ 45 ° j =   - 2 j + 5 cos ⁡ θ i - 5 sin ⁡ θ j

Para determinar v b a r c o , as equações acima devem ser separadas para i e j .

Para i ,

v b a r c o sin ⁡ 45 ° = 5 cos ⁡ θ

Para j ,

-   v b a r c o cos ⁡ 45 ° =   - 2 - 5 sin ⁡ θ

Passo 2

As duas equações a cima formam um sistema linear,

v b a r c o sin ⁡ 45 ° =   5 cos ⁡ θ   -   v b a r c o cos ⁡ 45 ° =   - 2 - 5 sin ⁡ θ  

Resolvendo o sitema temos,

θ = 28,57 °

v b a r c o = 6,21   m / s

Passo 3

Para determinar o tempo basta dividir a distacia percorrida pela velocidade escalar encontrada

t = S A B v b a r c o = 50 2 + 50 2 6,21 = 11,4   s

Resposta

A velocidade escalar do barco é v b a r c o = 6,21   m / s e sua direção θ = 28,57 ° e o tempo para o trajeto é 11 ,   4 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os satélites A e B estão em uma órbita circular de altitude h = 1500k m . Determine o módulo da aceleração do satélite B em relação a um observador sem rotação no satélite A . Utilize g 0 = 9,825m / s
A nave espacial S aproxima-se do planeta Marte ao longo de uma trajetória b - b no plano orbital de Marte com uma velocidade absoluta de 19k m / s . Marte tem uma velocidade de 24,1k m / s ao longo de
Um rebatedor acerta a bola de beisebol A com uma velocidade inicial de v 0 = 30m / s diretamente para o jogador B com um ângulo de 30 ° com a horizontal; a posição inicial da bola é 0,9m acima do níve
Em um dado instante após saltar do avião A , um paraquedista B está na posição mostrada e atingiu uma velocidade terminal (constante) v B = 50m / s . O avião possui a mesma velocidade constante v A =
O capitão de um pequeno navio capaz de atingir uma velocidade de 6 nós através de águas calmas deseja definir um curso que levará o barco diretamente para leste a partir de A até B por uma distância d