Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 61

a

Passo 1

E ai gurizada tudo certinho? O enunciado pede que a gente determine as tensões principais e a tensão de cisalhamento máxima no ponto a . Então ´partiu!!

Dobra: Ponta a   para no eixo neutro.

σ = 0

Torção: τ = T c 1 a b 2 onde a=b=d

E C 1 = 0,208   por seção quadrada

Desde T = P d 2 ,     τ T = P 0,416 d 2 = 2,404 P d 2

Passo 2

Para o cisalhamento Transverso temos... considere nosso lindo esboço

V = P         1 = 1 12 d 4

A = 1 2 d 2     y - = 1 4 d               Q = A y - = 1 8 d 3

t = d

τ V = V Q I t = 1,5 P d 2

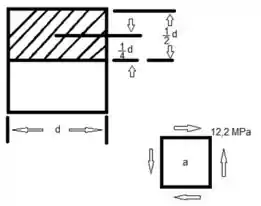
Passo 3

Por superposição,

τ = τ T + τ V = 3,904 P d 2

τ = 3,904 5 x 10 3 40 x 10 - 3 2 = 12,2 x 10 6 P a = 12,2 M P a

Círculo de Mohr’s σ M A X = 12,2 M P a

σ M I N = - 12,2 M P a

τ M A X = 12,2 M P a

Resposta

σ M I N = - 12,2 M P a

τ M A X = 12,2 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 8.26 para o ponto B .
Visto que o concreto só pode suportar pouca ou nenhuma tração, esse problema pode ser evitado se o concreto for protendido com cabos ou hastes. Considere a viga simplesmente apoiada mostrada na figura
A pilastra de alvenaria está sujeita à carga de 800kN . Determine a equação da reta y=f ( x ) ao longo da qual a carga pode ser posicionada sem provocar tensão de tração na pilastra. Despreze o peso d
O bloco está sujeito às duas cargas axiais mostradas figura. Determine a tensão normal desenvolvida nos pontos A e B . Despreze o peso do bloco.
O elo de metal está sujeito à força axial P=7kN . Sua seção transversal original deve ser alterada pelo corte de uma ranhura circular em um lado. Determine a distância a até onde a ranhura pode penetr