Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 16
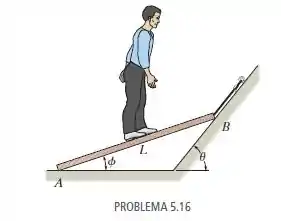
O homem tem um peso e se encontra no centro da tábua. Se os planos em e são lisos, determine a tração na corda em termos de e
Passo 1
É importante analisar corretamente os graus de liberdade de cada elemento de apoio. Para o nosso sistema temos que as reações serão somente normais e .
Observe o diagrama:
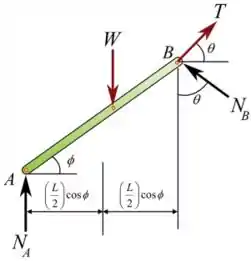
Feitas estas considerações, vamos aos cálculos.
Passo 2
Nós podemos aplicar o somatório de momentos em para descobrir :
Da análise das forças em , temos:
Da análise das forças em , temos:
Resposta
Exercícios de Livros Relacionados
Quando o corpo de 0,05k g está na posição mostrada, a mola linear é esticada 10m m . Determine a força P necessária para quebrar o contato em C . Soluções completas para ( a ) incluindo os efeitos do
O dobrador de tubos consiste em duas polias ranhuradas montadas e livres para girar em uma estrutura fixa. O tubo é dobrado na forma mostrada por uma força P = 300N . Calcule as forças suportadas pelo
A parte lombar da coluna vertebral humana suporta todo o peso da parte superior do tronco e a carga de força que lhe é imposta. Consideramos aqui o disco (sombreado em vermelho) entre a vértebra infer
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.1. Determine as componentes horizontal e vertical da reação dos apoios. Despreze a espessura da viga.
Todos as soluções dos problemas precisam incluir um diagrama de corpo livre.F5.5. A haste de 25 kg possui centro de massa em G. Se ela é sustentada por uma cavilha lisa em C, um rolete em A e a corda