A parte lombar da coluna vertebral humana suporta todo o peso da parte superior do tronco e a carga de força que lhe é imposta. Consideramos aqui o disco (sombreado em vermelho) entre a vértebra inferior da região lombar e a vértebra superior da região do sacro. Para o caso , determine a força de compressão e a força de cisalhamento suportada por este disco em termos do peso corporal . O peso da parte superior do tronco (acima do disco em questão) é 68% de o peso corporal total e atua no . A força vertical que os músculos retos das costas exercem na parte superior do tronco atua como mostrado na figura. Repita para o caso em que a pessoa tem um peso de magnitude conforme mostrado. Declare quaisquer suposições.
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força de compressão e a força de cisalhamento suportada pelo disco em duas situações: quando , ou seja, não há peso adicional e quando . Para resolver este problema vamos fazer o diagrama de corpo livre do sistema apenas com as forças e seus pontos de aplicação com relação a um sistema de eixos com origem no ponto de aplicação das forças e . Para a situação , temos:
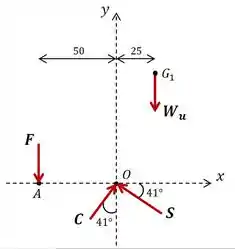
Este é um problema que pode ser facilmente resolvido pelas três equações de equilíbrio: somatório de forças nos eixos e e somatório de momentos. Vamos começar pelo momento em torno do , uma vez que isso elimina duas das nossas incógnitas:
Passo 2
Com isso, descobrimos a força que os músculos das costas exercem, mas ainda nos restam as forças de compressão e de cisalhamento que foram pedidas. Para encontra-las, podemos fazer o somatório de forças nas direções e que novamente devem ser nulos para que o sistema esteja em equilíbrio. Começando pela direção :
Vamos chamar essa equação de .
Agora para o eixo :
Substituindo o valor de da equação , temos:
Passo 3
Show de bola! Para resolver o item , precisamos primeiro incluir o carregamento em .
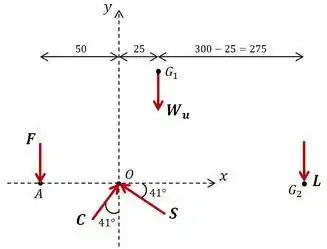
Bom, a partir daqui os cálculos são os mesmos. Vamos começar pelo momento em torno do , uma vez que isso elimina duas das nossas incógnitas:
Passo 4
E para determinar as forças de compressão e de cisalhamento , vamos novamente fazer o equilíbrio de forças nas direções e :
Vamos chamar essa equação de .
Agora para o eixo :
Substituindo o valor de da equação , temos:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" ![]()