Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 3
A inclinação da força de está especificada como mostrado na figura. Expresse como um vetor, em termos dos vetores unitários e .
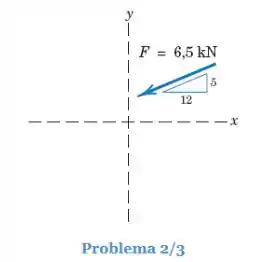
Passo 1
Olá, tudo bem com você?
Vamos começar a resolução destacando o ângulo que faz com o eixo . Observe que, no gráfico, deslocamos os eixos até para representar o ângulo e facilitar o entendimento.
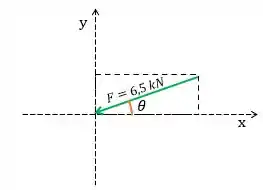
Através do Teorema de Pitágoras, encontramos a hipotenusa do triângulo retângulo:
Veja que o vetor aponta para o sentido negativo de e de . Temos que,
Passo 2
Em posse de tais dados, vamos calcular as componentes:
Passo 3
Agora, expressando como um vetor, em termos dos vetores unitários e :
Resposta
Exercícios de Livros Relacionados
Uma ponte rolante é usada para reposicionar o vagão dentro de uma oficina de reparos para vagões. Se o vagão começa a mover-se ao longo dos trilhos, quando a componente x da tensão do cabo alcança 3k
Determine o ângulo θ entre a força de 200N e a linha O C .
A força F tem um módulo de 2k N e é direcionado deA para B . Calcule a projeção F C Dd eF sobre a linha C D e determine o ângulo θ entre F e C D .
Determine o momento associado com o binário aplicado na placa retangular. Reconciliar os resultados com os casos individuais de θ=0 ,b=0eh=0 .
A força F tem um módulo de 500N e atua ao longo da diagonal da linha A M , em que M é o ponto médio do lado vertical O B do paralelepípedo. Expresse F em termos de seu módulo multiplicado pelo vetor u