Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 38

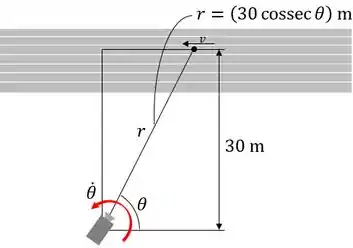
No instante que θ = 45 ° , o atleta está correndo com uma velocidade escalar constante de 2 m/s. Determine a velocidade angular na qual a câmera deve girar a fim de seguir o movimento.

Passo 1

O enunciado nos dá as seguintes informações:

Velocidade escalar do atleta: v = 2 m/s;

Trajetória da câmera: r = 30 cossec ⁡ θ m.

Devemos determinar a velocidade angular da câmera quando θ = 45 ° .

Passo 2

Sabemos que, por definição, a velocidade em coordenadas polares é composta por uma componente radial e uma componente transversal, conforme exibido abaixo:

v = v r 2 + v θ 2

Onde

v r = r ˙

v θ = r θ ˙

Substituindo esses valores na equação da velocidade e colocando θ ˙ evidência, ficamos com

v = v r 2 + v θ 2

v 2 = v r 2 + v θ 2

v θ = v 2 - v r 2

r θ ˙ = v 2 - r ˙ 2

θ ˙ = v 2 - r ˙ 2 r

Portanto, para descobrirmos o valor da velocidade angular, precisamos saber os valores de v , r e r ˙ .

Para θ = 45 ° ,   o valor de v e de r são conhecidos. Devemos então encontrar o valor de r ˙ .

Sabendo que r = 30 cossec ⁡ θ , sua derivada temporal será

r ˙ = d r d t = - 30 θ ˙ cossec ⁡ θ cotan ⁡ θ

r ˙ = - 30 θ ˙ sen ⁡ θ   1 tan ⁡ θ    

Em θ = 45 ° , temos

v = 2   m / s

r = 30 cossec ⁡ 45 ° = 30 sen ⁡ 45 ° = 42,426   m

r ˙ = - 30 θ ˙ sen ⁡ 45 ° 1 tan ⁡ 45 ° = - 42,426 θ ˙

Substituindo esses valores em

θ ˙ = v 2 - r ˙ 2 r

Obtemos

θ ˙ = 2 2 - ( - 42,426 θ ˙ ) 2 42,426

42,426   θ ˙ 2 = 2 2 - ( - 42,426 θ ˙ ) 2

42,426   θ ˙ 2 + ( - 42,426 θ ˙ ) 2 = 4

θ ˙ 2 = 4 2 ( 42,426 2 )

θ ˙ = 0,0333   r a d / s

Resposta

θ ˙ = 0,0333   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que o momento angular por unidade de massa h de um satélite que descreve uma órbita elíptica de semieixo maior a e excentricidade ε , em torno de um planeta de massa M, pode ser expresso como h
Um satélite descreve uma órbita elíptica em torno de um planeta. Representando por r0 e r1 as distâncias correspondentes, respectivamente, ao perigeu e ao apogeu da órbita, mostre que a curvatura da ó
Uma partícula de massa m descreve uma trajetória definida pela equação r = r 0 sen θ sob uma força central F voltada para o centro de força O. Mostre que F é inversamente proporcional àquinta potência
Uma partícula de massa m é lançada do ponto A com uma velocidade inicial v 0 perpendicular a OA e se move sob a ação de uma força central F ao longo de uma trajetória elíptica definida elaequação r =
Uma partícula de massa m descreve uma cardioide r = r 0 (1 cos θ /2) sob uma força central F voltada para o centro de força O. Usando a Eq. (12.37), mostre que F é inversamente proporcional ao quadrad